Skip to content

Latest commit

 

History

History
378 lines (318 loc) · 9.69 KB

README_EN.md

File metadata and controls

378 lines (318 loc) · 9.69 KB
comments difficulty edit_url tags
true
Medium
Array
Binary Search
Divide and Conquer
Matrix

240. Search a 2D Matrix II

中文文档

Description

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

  • Integers in each row are sorted in ascending from left to right.
  • Integers in each column are sorted in ascending from top to bottom.

 

Example 1:

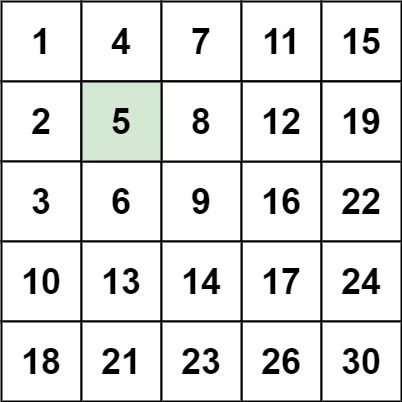
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -109 <= matrix[i][j] <= 109
  • All the integers in each row are sorted in ascending order.
  • All the integers in each column are sorted in ascending order.
  • -109 <= target <= 109

Solutions

Solution 1: Binary Search

Since all elements in each row are sorted in ascending order, we can use binary search to find the first element that is greater than or equal to target for each row, and then check if this element is equal to target. If it equals target, it means the target value has been found, and we directly return true. If it does not equal target, it means all elements in this row are less than target, and we should continue to search the next row.

If all rows have been searched and the target value has not been found, it means the target value does not exist, so we return false.

The time complexity is $O(m \times \log n)$, where $m$ and $n$ are the number of rows and columns in the matrix, respectively. The space complexity is $O(1)$.

Python3

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        for row in matrix:
            j = bisect_left(row, target)
            if j < len(matrix[0]) and row[j] == target:
                return True
        return False

Java

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for (var row : matrix) {
            int j = Arrays.binarySearch(row, target);
            if (j >= 0) {
                return true;
            }
        }
        return false;
    }
}

C++

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (auto& row : matrix) {
            int j = lower_bound(row.begin(), row.end(), target) - row.begin();
            if (j < matrix[0].size() && row[j] == target) {
                return true;
            }
        }
        return false;
    }
};

Go

func searchMatrix(matrix [][]int, target int) bool {
	for _, row := range matrix {
		j := sort.SearchInts(row, target)
		if j < len(matrix[0]) && row[j] == target {
			return true
		}
	}
	return false
}

TypeScript

function searchMatrix(matrix: number[][], target: number): boolean {
    const n = matrix[0].length;
    for (const row of matrix) {
        let left = 0,
            right = n;
        while (left < right) {
            const mid = (left + right) >> 1;
            if (row[mid] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        if (left != n && row[left] == target) {
            return true;
        }
    }
    return false;
}

Rust

use std::cmp::Ordering;

impl Solution {
    pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
        let m = matrix.len();
        let n = matrix[0].len();
        let mut i = 0;
        let mut j = n;
        while i < m && j > 0 {
            match target.cmp(&matrix[i][j - 1]) {
                Ordering::Less => {
                    j -= 1;
                }
                Ordering::Greater => {
                    i += 1;
                }
                Ordering::Equal => {
                    return true;
                }
            }
        }
        false
    }
}

JavaScript

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
    const n = matrix[0].length;
    for (const row of matrix) {
        let left = 0,
            right = n;
        while (left < right) {
            const mid = (left + right) >> 1;
            if (row[mid] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        if (left != n && row[left] == target) {
            return true;
        }
    }
    return false;
};

C#

public class Solution {
    public bool SearchMatrix(int[][] matrix, int target) {
        foreach (int[] row in matrix) {
            int j = Array.BinarySearch(row, target);
            if (j >= 0) {
                return true;
            }
        }
        return false;
    }
}

Solution 2: Search from the Bottom Left or Top Right

Here, we start searching from the bottom left corner and move towards the top right direction, comparing the current element matrix[i][j] with target:

  • If $\text{matrix}[i][j] = \text{target}$, it means the target value has been found, and we directly return true.
  • If $\text{matrix}[i][j] &gt; \text{target}$, it means all elements in this column from the current position upwards are greater than target, so we should move the $i$ pointer upwards, i.e., $i \leftarrow i - 1$.
  • If $\text{matrix}[i][j] &lt; \text{target}$, it means all elements in this row from the current position to the right are less than target, so we should move the $j$ pointer to the right, i.e., $j \leftarrow j + 1$.

If the search ends and the target is still not found, return false.

The time complexity is $O(m + n)$, where $m$ and $n$ are the number of rows and columns in the matrix, respectively. The space complexity is $O(1)$.

Python3

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        i, j = m - 1, 0
        while i >= 0 and j < n:
            if matrix[i][j] == target:
                return True
            if matrix[i][j] > target:
                i -= 1
            else:
                j += 1
        return False

Java

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int i = m - 1, j = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] == target) {
                return true;
            }
            if (matrix[i][j] > target) {
                --i;
            } else {
                ++j;
            }
        }
        return false;
    }
}

C++

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int i = m - 1, j = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] == target) {
                return true;
            }
            if (matrix[i][j] > target) {
                --i;
            } else {
                ++j;
            }
        }
        return false;
    }
};

Go

func searchMatrix(matrix [][]int, target int) bool {
	m, n := len(matrix), len(matrix[0])
	i, j := m-1, 0
	for i >= 0 && j < n {
		if matrix[i][j] == target {
			return true
		}
		if matrix[i][j] > target {
			i--
		} else {
			j++
		}
	}
	return false
}

TypeScript

function searchMatrix(matrix: number[][], target: number): boolean {
    const [m, n] = [matrix.length, matrix[0].length];
    let [i, j] = [m - 1, 0];
    while (i >= 0 && j < n) {
        if (matrix[i][j] === target) {
            return true;
        }
        if (matrix[i][j] > target) {
            --i;
        } else {
            ++j;
        }
    }
    return false;
}

C#

public class Solution {
    public bool SearchMatrix(int[][] matrix, int target) {
        int m = matrix.Length, n = matrix[0].Length;
        int i = m - 1, j = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] == target) {
                return true;
            }
            if (matrix[i][j] > target) {
                --i;
            } else {
                ++j;
            }
        }
        return false;
    }
}