Skip to content

Latest commit

 

History

History
268 lines (223 loc) · 8.95 KB

README_EN.md

File metadata and controls

268 lines (223 loc) · 8.95 KB
comments difficulty edit_url tags
true
Medium
Tree
Depth-First Search
Array
Dynamic Programming

3004. Maximum Subtree of the Same Color 🔒

中文文档

Description

You are given a 2D integer array edges representing a tree with n nodes, numbered from 0 to n - 1, rooted at node 0, where edges[i] = [ui, vi] means there is an edge between the nodes vi and ui.

You are also given a 0-indexed integer array colors of size n, where colors[i] is the color assigned to node i.

We want to find a node v such that every node in the subtree of v has the same color.

Return the size of such subtree with the maximum number of nodes possible.

 

Example 1:

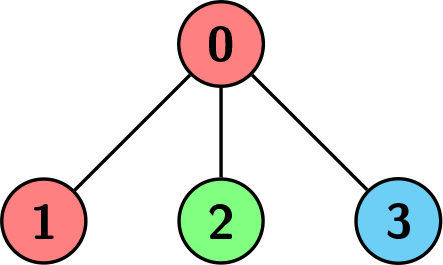
Input: edges = [[0,1],[0,2],[0,3]], colors = [1,1,2,3]
Output: 1
Explanation: Each color is represented as: 1 -> Red, 2 -> Green, 3 -> Blue. We can see that the subtree rooted at node 0 has children with different colors. Any other subtree is of the same color and has a size of 1. Hence, we return 1.

Example 2:

Input: edges = [[0,1],[0,2],[0,3]], colors = [1,1,1,1]
Output: 4
Explanation: The whole tree has the same color, and the subtree rooted at node 0 has the most number of nodes which is 4. Hence, we return 4.

Example 3:

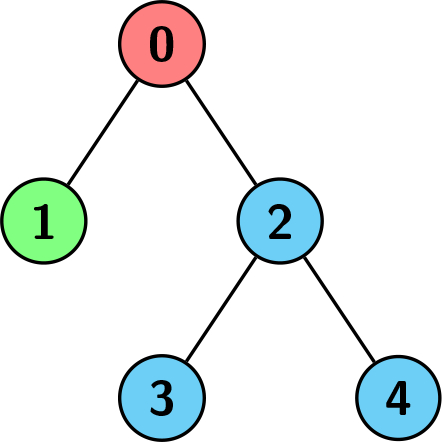
Input: edges = [[0,1],[0,2],[2,3],[2,4]], colors = [1,2,3,3,3]
Output: 3
Explanation: Each color is represented as: 1 -> Red, 2 -> Green, 3 -> Blue. We can see that the subtree rooted at node 0 has children with different colors. Any other subtree is of the same color, but the subtree rooted at node 2 has a size of 3 which is the maximum. Hence, we return 3.

 

Constraints:

  • n == edges.length + 1
  • 1 <= n <= 5 * 104
  • edges[i] == [ui, vi]
  • 0 <= ui, vi < n
  • colors.length == n
  • 1 <= colors[i] <= 105
  • The input is generated such that the graph represented by edges is a tree.

Solutions

Solution 1: DFS

First, according to the edge information given in the problem, we construct an adjacency list $g$, where $g[a]$ represents all adjacent nodes of node $a$. Then we create an array $size$ of length $n$, where $size[a]$ represents the number of nodes in the subtree with node $a$ as the root.

Next, we design a function $dfs(a, fa)$, which will return whether the subtree with node $a$ as the root meets the requirements of the problem. The execution process of the function $dfs(a, fa)$ is as follows:

  • First, we use a variable $ok$ to record whether the subtree with node $a$ as the root meets the requirements of the problem, and initially $ok$ is $true$.
  • Then, we traverse all adjacent nodes $b$ of node $a$. If $b$ is not the parent node $fa$ of $a$, then we recursively call $dfs(b, a)$, save the return value into the variable $t$, and update $ok$ to the value of $ok$ and $colors[a] = colors[b] \land t$, where $\land$ represents logical AND operation. Then, we update $size[a] = size[a] + size[b]$.
  • After that, we judge the value of $ok$. If $ok$ is $true$, then we update the answer $ans = \max(ans, size[a])$.
  • Finally, we return the value of $ok$.

We call $dfs(0, -1)$, where $0$ represents the root node number, and $-1$ represents that the root node has no parent node. The final answer is $ans$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes.

Python3

class Solution:
    def maximumSubtreeSize(self, edges: List[List[int]], colors: List[int]) -> int:
        def dfs(a: int, fa: int) -> bool:
            ok = True
            for b in g[a]:
                if b != fa:
                    t = dfs(b, a)
                    ok = ok and colors[a] == colors[b] and t
                    size[a] += size[b]
            if ok:
                nonlocal ans
                ans = max(ans, size[a])
            return ok

        n = len(edges) + 1
        g = [[] for _ in range(n)]
        size = [1] * n
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = 0
        dfs(0, -1)
        return ans

Java

class Solution {
    private List<Integer>[] g;
    private int[] colors;
    private int[] size;
    private int ans;

    public int maximumSubtreeSize(int[][] edges, int[] colors) {
        int n = edges.length + 1;
        g = new List[n];
        size = new int[n];
        this.colors = colors;
        Arrays.fill(size, 1);
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1);
        return ans;
    }

    private boolean dfs(int a, int fa) {
        boolean ok = true;
        for (int b : g[a]) {
            if (b != fa) {
                boolean t = dfs(b, a);
                ok = ok && colors[a] == colors[b] && t;
                size[a] += size[b];
            }
        }
        if (ok) {
            ans = Math.max(ans, size[a]);
        }
        return ok;
    }
}

C++

class Solution {
public:
    int maximumSubtreeSize(vector<vector<int>>& edges, vector<int>& colors) {
        int n = edges.size() + 1;
        vector<int> g[n];
        vector<int> size(n, 1);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int ans = 0;
        function<bool(int, int)> dfs = [&](int a, int fa) {
            bool ok = true;
            for (int b : g[a]) {
                if (b != fa) {
                    bool t = dfs(b, a);
                    ok = ok && colors[a] == colors[b] && t;
                    size[a] += size[b];
                }
            }
            if (ok) {
                ans = max(ans, size[a]);
            }
            return ok;
        };
        dfs(0, -1);
        return ans;
    }
};

Go

func maximumSubtreeSize(edges [][]int, colors []int) (ans int) {
	n := len(edges) + 1
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	size := make([]int, n)
	var dfs func(int, int) bool
	dfs = func(a, fa int) bool {
		size[a] = 1
		ok := true
		for _, b := range g[a] {
			if b != fa {
				t := dfs(b, a)
				ok = ok && t && colors[a] == colors[b]
				size[a] += size[b]
			}
		}
		if ok {
			ans = max(ans, size[a])
		}
		return ok
	}
	dfs(0, -1)
	return
}

TypeScript

function maximumSubtreeSize(edges: number[][], colors: number[]): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const size: number[] = Array(n).fill(1);
    let ans = 0;
    const dfs = (a: number, fa: number): boolean => {
        let ok = true;
        for (const b of g[a]) {
            if (b !== fa) {
                const t = dfs(b, a);
                ok = ok && t && colors[a] === colors[b];
                size[a] += size[b];
            }
        }
        if (ok) {
            ans = Math.max(ans, size[a]);
        }
        return ok;
    };
    dfs(0, -1);
    return ans;
}