SVM.md

SVM

Q1.什么是SVM？

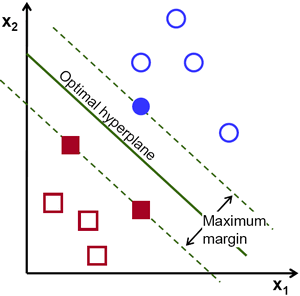
• 支持向量机 (SVM)是一种用于分类、回归和异常值检测的监督学习方法。支持向量机算法的目标是在 N 维空间（N — 特征数）中找到一个超平面，该超平面可以在特征空间上使两类数据间隔最大。
• 支持向量机只关注最难区分的点（支持向量），而其他分类器关注所有的点。

Q2:SVM中的超平面是什么？

• 超平面是帮助对数据点进行分类的决策边界。落在超平面两侧的数据点可以归为不同的类别。此外，超平面的维数取决于特征的数量。如果输入特征的数量是 2，那么超平面就是一条直线。如果输入特征的个数是3，那么超平面就变成了一个二维平面。
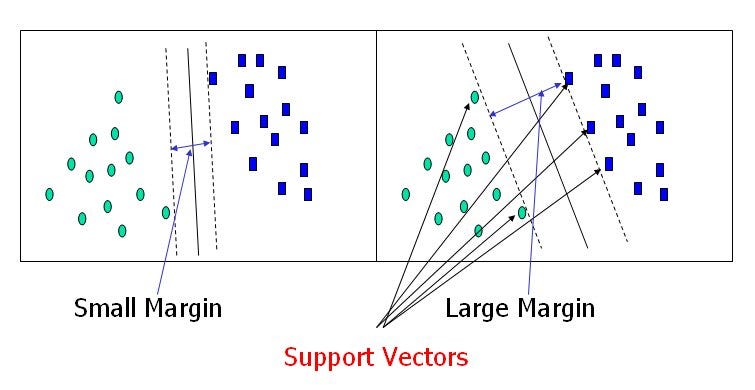
• 为了分离两类数据点，可以选择许多可能的超平面。我们的目标是找到一个具有最大边距的平面，即两个类的数据点之间的最大距离。

Q3:SVM 中的支持向量是什么？

• 支持向量是最接近超平面的数据点，数据集的点如果被移除，将改变分割超平面的位置。使用这些支持向量，我们最大化分类器的边缘。对于计算预测，仅使用支持向量。

Q4:什么是hard-margin和soft-margin SVM？

• Hard-Margin SVM 具有线性可分的训练数据。边缘区域不允许有数据点。这种类型的线性分类称为硬间隔分类。
• Soft-Margin SVM 具有非线性可分的训练数据。Margin violation 意味着选择一个超平面，它可以让一些数据点停留在 margin 区域之间或超平面的错误一侧。

Q5:你知道哪些类型的SVM内核？

• 一般有线性核、多项式核、高斯核

Q6:为什么使用核技巧？

• SVM在处理非线性可分的数据时，需要使用核函数将数据从低维转到更高的维度以便于找到边界并进行分类；但在维度越来越多时，计算代价将会非常昂贵。核技巧允许我们在原始特征（低维度）上进行计算，而将实质上的分类效果（利用了内积）表现在了高维上，这样避免了直接在高维空间中的复杂计算，真正解决了SVM线性不可分的问题

Q7:SVM有哪些应用？

SVM 依赖于监督学习算法。使用 SVM 的目的是对看不见的数据进行正确*分类。*SVM 的一些常见应用是：

• 人脸检测——SVMc 将图像的一部分分类为人脸和非人脸，并在人脸周围创建方形边界。
• 文本和超文本分类——支持向量机允许对归纳和转导模型进行文本和超文本分类。他们使用训练数据将文档分类为不同的类别。它根据生成的分数进行分类，然后与阈值进行比较。
• 图像分类——使用支持向量机可以为图像分类提供更好的搜索精度。与传统的基于查询的搜索技术相比，它提供了更高的准确性。
• 生物信息学——它包括蛋白质分类和癌症分类。我们使用 SVM 来识别基因的分类、基于基因的患者和其他生物学问题。
• 蛋白质折叠和远程同源检测——应用 SVM 算法进行蛋白质远程同源检测。
• 手写识别——我们使用支持向量机来识别广泛使用的手写字符。
• 广义预测控制 (GPC) – 使用基于 SVM 的 GPC 来控制具有有用参数的混沌动力学。

Q8:说出SVM的一些优点？

• 保证最优性：由于凸优化的性质，解决方案将始终是全局最小值而不是局部最小值。
• 丰富的实现：我们可以方便地访问它，无论是从 Python 还是 Matlab。
• SVM 可用于线性可分离和非线性可分离的数据。线性可分数据是硬边界，而非线性可分数据是软边界。
• SVM符合半监督学习模型。它可用于数据已标记和未标记的区域。它只需要一个最小化问题的条件，称为 Transductive SVM。
• Feature Mapping过去对模型的整体训练性能的计算复杂度造成了很大的负担。然而，在Kernel Trick的帮助下，SVM 可以使用简单的点积进行特征映射。

Q9:对于N维度数据集，支持向量的最小可能数量是多少？(假设数据是完全线性可分的)

• 无论数据集的维数或大小如何，支持向量的数量都可以少至2.

Q10:当 SVM 中没有明确的超平面时会发生什么？

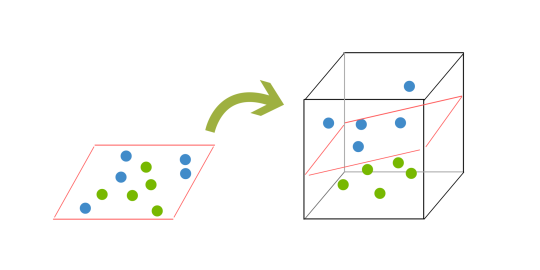
• 数据很少像超平面那样干净，超平面是一条线性分离和分类一组数据的线。为了对数据集进行分类，有必要从数据的 2D 视图转移到 3D 视图。
• 数据点的这种“提升”表示将数据映射到更高的维度。这被称为核化。

Q11:SVM中的hinge loss是什么？

• 合页损失函数，主要与软间隔支持向量机有关。它将分类边界的边际或距离纳入成本计算。即使新的观测值被正确分类，如果与决策边界的距离不够大，它们也会受到惩罚。铰链损失线性增加。

• 引入hingle loss的主要目的是惩罚软间隔SVM中被错误分类的样本

• hingle loss的公式是：,第一项是错误分类损失，第二项为分类间隔margin距离

  

引用：https://programmathically.com/understanding-hinge-loss-and-the-svm-cost-function/

Q12：超参数C在SVM中的作用

• C: 目标函数的惩罚系数C，用在软间隔SVM中，用来平衡分类间隔margin和错分样本损失；

Q13: 讲述设计SVM分类器时常用的超参数

• SVM模型有两个非常重要的参数C与gamma。其中 C是惩罚系数，即对误差的宽容度。c越高，说明越不能容忍出现误差,容易过拟合。C越小，容易欠拟合。C过大或过小，都会导致泛化能力变差；gamma是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度。

Q14:比较KNN算法和SVM算法

• KNN没有训练过程，只是将训练数据与训练数据进行距离度量来实现分类；SVM需要训练，确定超平面的参数；
• KNN预测时要用到全部训练样本点，属于非稀疏模型；SVM只用到支持向量，属于稀疏模型；
• KNN只有一个参数k，SVM的参数更多，包括松弛变量的系数和具体的核函数；

Q15:使用SVM做分类和回归有什么区别？

• SVR回归与SVM分类的区别在于，SVR的样本点最终只有一类，它所寻求的最优超平面不是SVM那样使两类或多类样本点分的“最开”，而是使所有的样本点离着超平面的总偏差最小。
• SVM是要使到超平面最近的样本点的“距离”最大；SVR则是要使到超平面最远的样本点的“距离”最小。引用：https://www.cnblogs.com/belter/p/8975606.html

引用：https://www.quora.com/What-is-the-main-difference-between-a-SVM-and-SVR

Q16:什么是凸包？

• 一组点的凸包被定义为最小的凸多边形，它包围了集合中的所有点。凸意味着多边形没有向内弯曲的角。如下图，左边是凸多边形，右边是非凸多边形。

  

Q17：如何使用SVM进行异常检测？

• 使用one-class SVM，对数据中的异常点进行异常检测。其基本思想是，用SVM训练一个超球面，将正常数据和异常数据划分开：如果数据在超球面内，则判定为属于该数据分布；反之，则判定为离群点。

Q18: 比较SVM和logistic回归

• 都是监督学习的分类模型
• LR对异常值敏感；SVM对异常值不敏感。SVM 只考虑局部的边界线附近的点，而逻辑回归考虑全局（远离的点对边界线的确定也起作用，虽然作用会相对小一些）。LR模型找到的那个超平面，是尽量让所有点都远离他，而SVM寻找的那个超平面，是只让最靠近中间分割线的那些点尽量远离，即只用到那些支持向量的样本
• 损失函数不同，logistic回归使用交叉熵损失，SVM使用hinge loss
• 计算复杂度不同，对于海量数据，SVM 的效率较低，LR 的效率比较高
• 对非线性问题的处理方式不同，LR 主要靠特征构造，必须组合交叉特征、特征离散化，SVM主要通过核技巧

Q19：解释什么是核技巧

• 对于非线性可分的训练集，需要通过核函数将其非线性映射到高维空间来转化成线性可分的数据集；在维度很高时，需要分别计算映射后的向量、，再计算两者内积（需要计算内积是因为SVM求解公式中包含内积操作），计算复杂度很高；

  

  

  

• 核技巧是指找到一个核函数，使得，这样只需要在低维空间里计算核函数的值即可，而不需要先把数据映射到高维空间，节省大量运算。

  

引用：https://www.fanyeong.com/2017/11/13/the-kernel-trick/

Q20:比较随机森林和SVM，什么情况下优先使用随机森林（或svm）？

• 支持向量机在存在较少极值的小数据集上具有优势，随机森林则需要更多数据但一般可以得到非常好的且具有鲁棒性的模型。
• SVM没有处理缺失值的策略，而决策树有（缺失数据是指缺失某些特征数据，向量数据不完整,SVM需要在特征空间上寻找可分平面，受缺失数据影响大）

Q21:比较svm和deep learning

• 直观区别：deep learning是将许多神经网络层堆叠起来，以分层的方式学习越来越多的数据的抽象表示；而SVM是在数据点中找到一个分裂边界（线性可分情况下的超平面），该边界与任一类别的支持向量尽可能远；
• deep learning相对来说不可被解释，而SVM有强有力的数学推导支撑；
• 对权重初始化的敏感性：因为神经网络使用梯度下降，这使得它们对其权重矩阵的初始随机化敏感。这是因为，如果初始随机化使神经网络接近优化函数的局部最小值，则准确度将永远不会增加超过某个阈值。相反，SVM 更可靠，无论其初始配置如何，它们都能保证收敛到全局最小值。
• 在多类别问题上，deep learning更方便；SVM需要使用多个SVM分类器来处理多分类问题，而deep learning只需要单个神经网络。
• 在特征数大于样本数时，SVM表现不佳；SVM需要在特征工程上做更多的工作；

Q22:哪些情况不适合用SVM?

• 如果特征维度远远大于样本数，则SVM表现一般。
• SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。
• 存在大量缺失数据（指缺失某些特征数据，向量数据不完整）时，SVM希望样本在特征空间中线性可分，所以特征空间的好坏对SVM的性能很重要。缺失特征数据将影响训练结果的好坏。
• 多分类问题

Q23:解释什么是支持向量？

• 支持向量是最接近分隔超平面的数据点，数据集的点如果被移除，将改变分割超平面的位置。使用这些支持向量，我们最大化分类器的边缘。对于计算预测，仅使用支持向量。

Q24:提供软间隔支持向量机 (SVM)的直观解释

Q25:解释SVM中的凸优化问题

• 凸优化的目标就是解决带约束条件函数的极值问题，通用模型是,需同时满足以下三个条件：是凸函数，是凸函数，是仿射函数；

  

  

  

  

• SVM的初始问题为,其中为典型的凸函数，约束条件最高阶只有一阶，确实是仿射函数；因此初始问题为凸优化问题，可以通过拉格朗日法转换为无约束问题后，对其对偶问题求解。

  

  

Q26:什么是多项式内核？

• 多项式核依靠多项式函数，将数据映射到高维空间，使得原本线性不可分的数据线性可分，数学形式为

  

• 多项式核函数可以实现将低维的输入空间映射到高维的特征空间，适合于正交归一化（向量正交且模为1）数据，属于全局核函数，允许相距很远的数据点对核函数的值有影响。参数p越大，映射的维度越高，导致更复杂的模型，可能会过拟合。相反地，参数p过小会导致欠拟合。

引用：https://www.pycodemates.com/2022/10/svm-kernels-polynomial-kernel.html

Q27***:什么是高斯（RBF）核函数?***

• 高斯核函数会将原始空间映射到无穷维空间，数学形式为，由于函数形状接近高斯分布，称为高斯核函数;

  

• 高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么样的核函数的时候优先使用高斯核函数。

Q28:决策边界和超平面有什么区别?

• 超平面是一个空间的子空间，它是维度比所在空间小一维的空间。 如果数据空间本身是三维的， 则其超平面是二维平面，而如果数据空间本身是二维的，则其超平面是一维的直线。
• 决策边界是超平面的子集，在二分类问题中，如果一个超平面能够将数据划分为两个集合，其中每个集合中包含单独的一个类别，我们就 说这个超平面是数据的“决策边界”。

Q29:冗余数据会怎样影响SVM的性能？

• 数据集中的冗余数据/特征可能会使得SVM的分类性能变差，冗余特征会使得原数据映射至高维时引入许多不必要的噪声累积，对SVM的分类面选择产生不利影响。

引用：https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4709852/

Q30:阐述拉格朗日方法在SVM算法中的作用

• 拉格朗乘子法将SVM中的带约束凸二次规划问题转化为无约束问题，随后根据slater条件将其转化为拉格朗日对偶问题，由KKT条件求解原始问题中的w,b参数；

Q31:解释对偶问题在SVM中的作用

• 拉格朗日对偶的重要作用是将w，b的计算提前并消除w,b，使得优化函数变为拉格朗日乘子的单一参数优化问题，使得问题更容易求解
• 对偶问题自然地引入核函数，进而推广到非线性分类问题

Q32:超参数C的值如何影响 SVM?

• 当惩罚系数C比较大时，我们的损失函数也会越大，这意味着我们不愿意放弃比较远的离群点。这样我们会有更加多的支持向量，也就是说支持向量和超平面的模型也会变得越复杂，也容易过拟合。
• 当惩罚系数C比较小时，意味我们不想理那些离群点，会选择较少的样本来做支持向量，最终的支持向量和超平面的模型也会简单。scikit-learn中C的默认值是1

Q33:超参数gamma的值如何影响 SVM?

• 当γ比较小时，单个样本对整个分类超平面的影响比较小，不容易被选择为支持向量
• 当γ比较大时，单个样本对整个分类超平面的影响比较大，更容易被选择为支持向量**，或者说整个模型的支持向量也会多。scikit-learn中默认值是1/n_features

Q34:支持向量数与SVM分类器性能之间是否存在关系?

• 支持向量数越多，模型越复杂，SVM越容易过拟合
• 支持向量数越少，模型越简单，SVM越容易欠拟合

Q35:什么是结构化支持向量机？

• 结构 SVM 是 SVM 的推广，与仅考虑单变量预测（如分类和回归）的常规 SVM 不同，结构化SVM允许结构化输出（例如，树，序列，集合）。

Q36:解释SMO算法的思想；

• 简单：SMO算法将大优化的问题分解成多个小优化的问题。这些小问题往往比较容易求解，并且对他们进行顺序求解的结果与将他们作为整体来求解的结果完全一致
• 详细：SMO算法是一种启发式算法，其基本思路是：如果所有变量的解都满足此最优化问题的KKT条件（Karush-Kuhn-Tucker conditions)，那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件。否则，选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小。重要的是，这时子问题可以通过解析方法求解，这样就可以大大提高整个算法的计算速度。

Q37:说出使用支持向量机与逻辑回归进行分类时，分别的优势

• SVM受数据中异常点影响小，因为它只关心最接近决策边界的点；而逻辑回归关注所有数据，容易受异常点影响
• 逻辑回归训练速度快，适合大批量的训练数据
• 对于非线性数据空间，SVM更快（可以用核技巧优化运算）

Q38***:什么情况下使用SVM，什么情况下使用逻辑回归***？

• 数据中存在较多异常点/离群点时，使用SVM
• 当特征维度远大于数据样本数时，使用逻辑回归；特征维度较大时，使用SVM
• 在处理大批量数据时，SVM效率不高

Q39:SVM中的松弛变量是什么？

• 硬间隔SVM的约束条件是$y_{i}(wx_{i}+b)\geq 1$，软间隔SVM为了处理非严格线性可分的数据，引入松弛变量$\xi {i}$，引入后的约束条件是$y{i}(wx_{i}+b)\geq\xi _{i}$
• 松弛变量$\xi _{i}$是数据点到其分隔边界的函数距离，原来要求的是数据点到分界面的函数距离要大于等于1，现在就放宽到了数据点到分界面函数距离大于等于$1-\xi _{i}$，这是对异常离群点的一种容忍。

Q40:SVM中参数C和gamma的含义

• C又称惩罚因子，是SVM中控制误差的参数，软间隔SVM的优化目标为$min\frac{1}{2}w^{T}w+C\sum_{i=1}^{n}\xi _{i}$，C越大代表模型越关注那些被误分类的点；
• gamma参数是高斯内核的参数，Gamma 决定了SVM在决策边界中需要多少曲率，Gamma越大意味着更大的曲率，Gamma 越低意味着曲率较小。

引用：https://www.quora.com/What-are-C-and-gamma-with-regards-to-a-support-vector-machine

Q41:您将如何使用SVM处理非线性可分数据的分类

• 加入松弛变量和惩罚因子，找到“相对最好”的超平面，尽可能地将数据分类正确；
• 将低维数据（线性不可分）映射到高维空间中，使得在高维空间中数据是线性可分的，并引入核函数解决高维计算复杂的问题

Q42:能直观地解释一下PAC学习理论吗？

• PAC(Probably Approximately Correct) 为可能近似正确学习理论，主要思想是：由于我们不知道真实的数据分布，也不知道真实的目标函数，因此期望从有限的训练样本上学习到一个期望错误为0 的函数是不切实际的；需要降低对学习算法能力的期望，只要求学习算法可以以一定的概率学习到一个近似正确的假设；
• 一个PAC 可学习（PACLearnable）的算法是指该学习算法能够在多项式时间内从合理数量的训练数据中学习到一个近似正确的概率分布
• PAC 学习理论可以帮助分析一个机器学习方法在什么条件下可以学习到一个近似正确的分类器；如果希望模型的假设空间越大，泛化错误越小，其需要的样本数量越多。

Q43:支持向量机可以用于异常值检测吗？

• 可以，使用one-class SVM；在异常检测的场景下，one-class SVM通过寻找一个超平面，学习目标是最大化分离超平面到零点的距离；超平面将样本中的正例圈出来，用这个圈来判断一个新数据是否为正样本。如果在圈内，即为正样本，如果在圈外，即为异常值

Q44:SVM是否会遭受维度灾难?

• 维度灾难即为了获得更好的分类效果，我们需要添加更多的特征。而随着特征的增多，尽管分类器拟合的结果更加准确，但是计算量会显著增加，并且数据在空间中的密度会急剧减小。此时的分类器会把噪声也一并学习了，因此会出现过拟合；
• SVM通过核技巧，将高维运算用低维度核函数等效，避免了计算量的增加；但难以避免维度灾难中的过拟合问题

Q45:什么是Mercer 定理，它与 SVM 有什么关系?

• Mercer定理定义了核函数的必要条件：K是有效的核函数 ==> 核函数矩阵K是对称半正定的
• Mercer定理表明为了证明$K$是有效的核函数，那么我们不用去寻找映射函数$\phi$ ，而只需要在训练集上求出各个$K_{ij}$，然后判断矩阵$K$是否是半正定（使用左上角主子式大于等于零等方法）即可。

Q46:使用SVM时，如何优化RBF 内核，以适应大量训练样本？

• 通过使用Random Features，核方法可以扩展到大规模数据集上；该方法源自NIPS 2017的《Random Features for Large-Scale Kernel Machines》，其基本思想是，构造一个“随机”映射$z:R^{d}\rightarrow R^{D}$ 直接将数据映射到高维空间，使得在这空间上的内积可以近似等于核函数$K(x,y)$，特征映射可由MC采样方法近似；在$R^{D}$空间做线性SVM就能够有效扩展到大规模数据集上，计算和存储对于数据是线性的。

引用：https://maelfabien.github.io/machinelearning/largescale/

https://www.zhihu.com/question/19591450

Q47:为什么SVM现在不流行了？

• 目前是大数据时代，学习样本普遍是海量级别的，SVM由于其在大样本时超级大的计算量，热度有所下降

Q48:SVM什么时候表现不好？

• SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用
• 如果特征维度远远大于样本数，则SVM表现一般
• 在数据中有大量缺失数据时

Q49:SVM如何选择内核?

• 如果特征维数很高，往往线性可分（SVM解决非线性分类问题的思路就是将样本映射到更高维的特征空间中），可以采用LR或者线性核的SVM；
• 如果样本数量很多，由于求解最优化问题的时候，目标函数涉及两两样本计算内积，使用高斯核明显计算量会大于线性核，所以手动添加一些特征，使得线性可分，然后可以用LR或者线性核的SVM；
• 如果不满足上述两点，即特征维数少，样本数量正常，可以使用高斯核的SVM。