탐색 알고리즘 : DFS & BFS
DFS & BFS는 많은 양의 데이터 중 원하는 데이터를 찾는 탐색에 적합한 알고리즘이다.
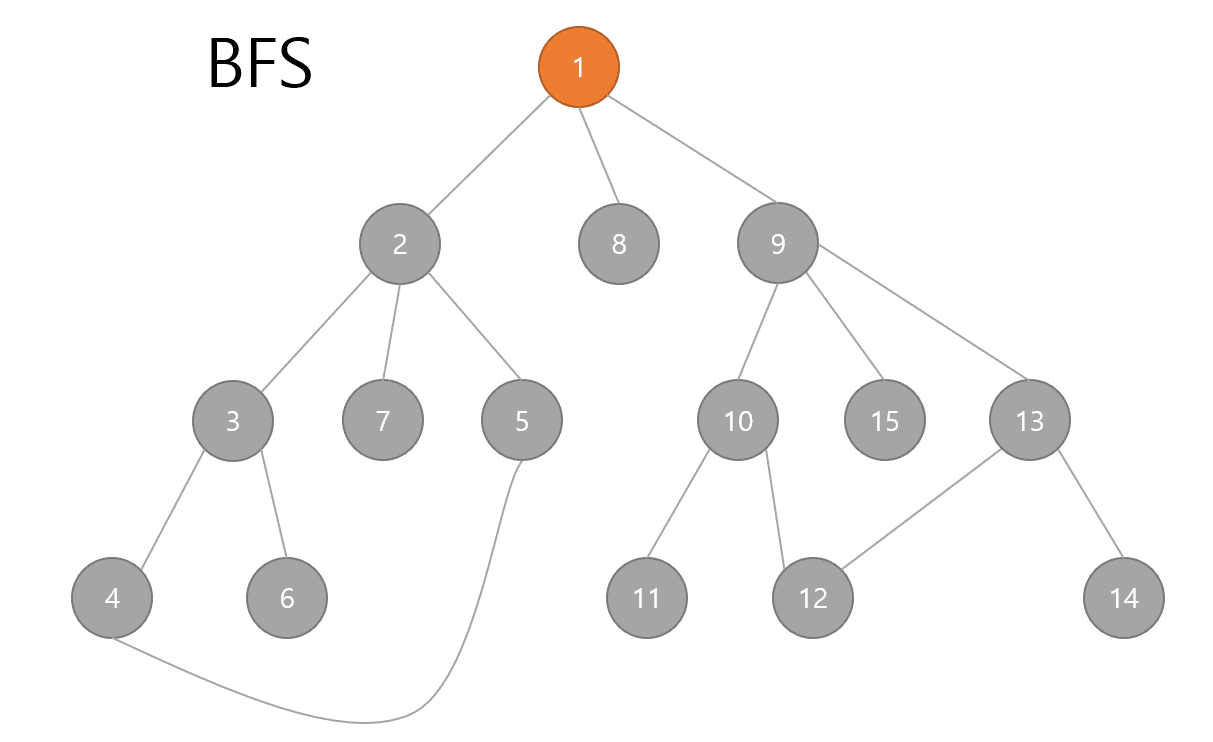
너비우선탐색으로 그래프에서 가장 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
BFS는 큐를 이용한다.
일단 BFS의 탐색 플로우는 다음과 같다.
- 탐색 시작노드를 큐에 삽입 & 방문처리
- 큐에서 노드를 꺼내고, 해당노드의 인접노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리
- 더 이상 방문 할 정점이 없으면 한 depth 내려가서 다시 인접한 모든 정점들을 우선 방문한다
val queue = LinkedList<Int>()
// queue : 이웃 자식이 어떤 것인지 탐색하고 다음으로 찾아야 할 자식을 알아둡니다.
val visited = ArrayList<Vertex<T>>()
//Visited : 어떤 정점이 접근되었는지 확인합니다.
fun bfs(start: Int) {
queue.add(start)
visited[start] = true
while (queue.isNotEmpty()) {
val head = queue.poll() // 첫 원소 반환 후 remove
for (next in edges[head]) {
if (!visited[next]) {
visited[next] = true
queue.add(next)
}
}
}
}- 최소신장 트리 Minimum-spanning-tree
- 정점사이 path 찾기
- 정점 사이 가장 짧은 거리 구하기
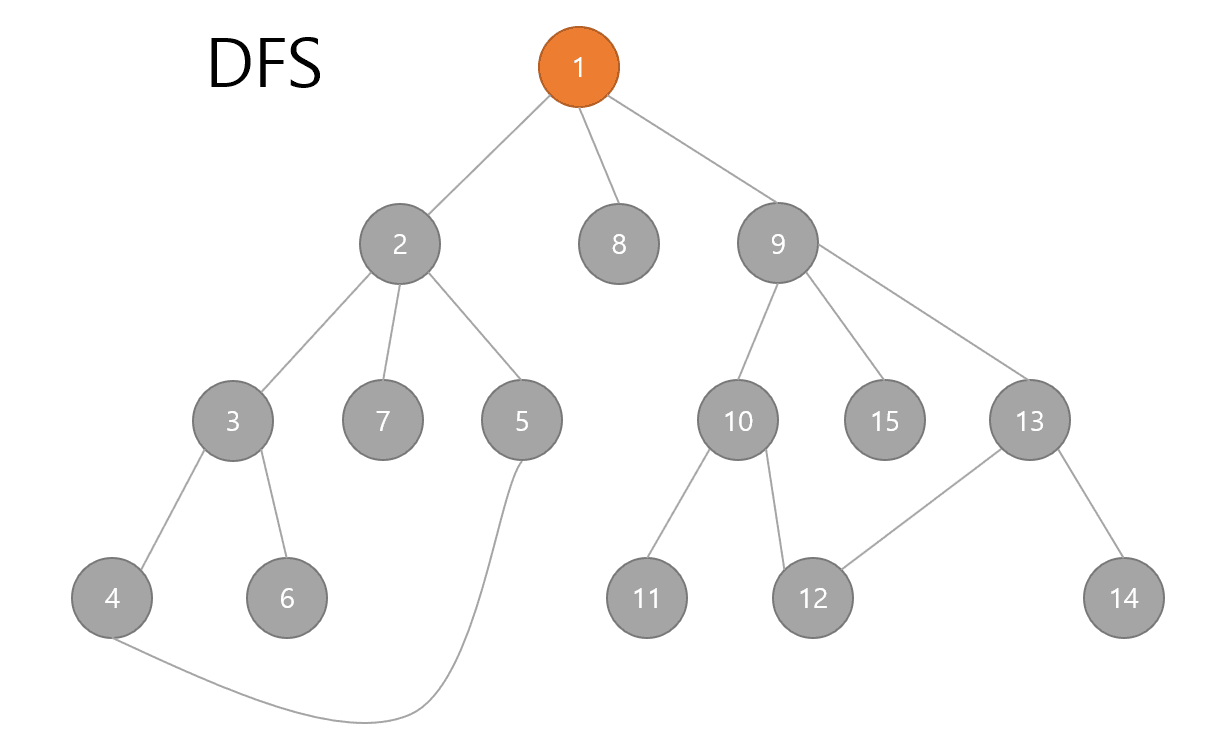
깊이우선 탐색으로 가장 깊은곳까지 먼저 탐색하는 알고리즘이다.
DFS는 스택자료구조(혹은 재귀함수)를 이용한다. 이때 주의 사항은 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다
- 시작노드를 스택에 삽입 / 방문처리
- 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문처리한다.
- 방문하지 않은 인접노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복
fun dfs(index: Int) {
visited[index] = true
// 구현
for (next in edges[index]) {
if (!visited[next]) {
dfs(next)
}
}
}- 그래프의 모든 정점을 방문하는 문제
- 경로들을 특징해서 저장해야 하는 문제
- 검색 대상의 그래프가 많이 큰 경우
- 사이클이 존재하는 경로를 찾는 경우
두 방식 모두 그래프 G = (V,E)의 모든 간선을 조회하기 때문에
인접 리스트로 표현된 그래프는 O(V+E) 인접 행렬로 표현된 그래프는 O(V^2)
간선 E의 개수가 노드 V의 개수보다 적은 게 일반적이기 때문에 인접 리스트 방식을 이용하는 것이 더 효율적이다.
모든 정점을 방문하는 것이 포인트인 문제는 두 가지 모두 사용가능하다.
하지만
경로의 특징을 저장해야 하는 경우 : DFS
최단 거리를 구해야 하는 경우 : BFS
사용하는 것이 바람직 하다.
또한 검색 대상의 그래프 규모가 크다면 : DFS 를 이용하는 게 효율적이다.
BFS에서 enqueue를 사용하기 때문에 이 작업을 할 때 걸리는 속도는 O(V)입니다. 모든 변을 접근할 때는 O(E). 그러므로 BFS의 전체적인 속도는 O(V+E)입니다.
이미지 출처 : https://toonraon.tistory.com/44