const rules = {
option1: { rule1: "value1", rule2: "value2" },
option2: { rule1: "value3", rule2: "value4" },
option3: { rule1: "value5", rule2: "value6" }
};Example 1
const rules = {
rock: { beats: "scissors", losesTo: "paper" },
paper: { beats: "rock", losesTo: "scissors" },
scissors: { beats: "paper", losesTo: "rock" }
};Example 2
const rules = {
name: { required: true, maxLength: 50 },
email: { required: true, emailFormat: true },
age: { required: true, minValue: 18, maxValue: 100 },
password: { required: true, minLength: 8, hasNumber: true, hasSpecialChar: true }
};function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let current = arr[i];
let j = i - 1;
// Shift elements to the right until the correct position for 'current' is found
while (j >= 0 && arr[j] > current) {
arr[j + 1] = arr[j];
j--;
}
// Place 'current' in its correct position
arr[j + 1] = current;
}
return arr;
}
let array = [5, 3, 8, 4, 2];
console.log(insertionSort(array)); // Output: [2, 3, 4, 5, 8]Merge sort is a sorting algorithm that works by dividing a list into smaller parts, sorting them, and then combining them back together in a sorted order. The process involves two main steps:
Divide: Split the list in half repeatedly until you have lists with only one element each. These one-element lists are considered sorted. Merge: Combine these small sorted lists back together by comparing and merging pairs of adjacent lists, resulting in a single sorted list. This process continues recursively until the original list is completely sorted.
// The mergeSort function is the main sorting function.
function mergeSort(arr) {
// Base case: If the array has 1 or 0 elements, it's already sorted.
if (arr.length <= 1) {
return arr;
}
// Find the middle index of the array.
const middle = Math.floor(arr.length / 2);
// Split the array into two parts: left and right.
const left = arr.slice(0, middle);
const right = arr.slice(middle);
// Recursively sort both the left and right parts of the array,
// then merge them back together.
return merge(mergeSort(left), mergeSort(right));
}
// The merge function combines two sorted arrays (left and right) into a single sorted array.
function merge(left, right) {
const result = [];
// The while loop continues as long as both left and right arrays have elements.
while (left.length && right.length) {
// Compare the first elements of left and right arrays.
// If the first element in the left array is smaller,
// remove it from the left array using shift() and push it to the result array.
// Otherwise, remove the first element from the right array and push it to the result array.
result.push(left[0] < right[0] ? left.shift() : right.shift());
}
// At this point, either the left or right array is empty (or both).
// Concatenate any remaining elements from left and right arrays to the result array.
// Since left and right arrays are already sorted, this step maintains the sorted order.
return [...result, ...left, ...right];
}
// Usage example
const unsortedArray = [34, 7, 23, 32, 5, 62];
const sortedArray = mergeSort(unsortedArray);
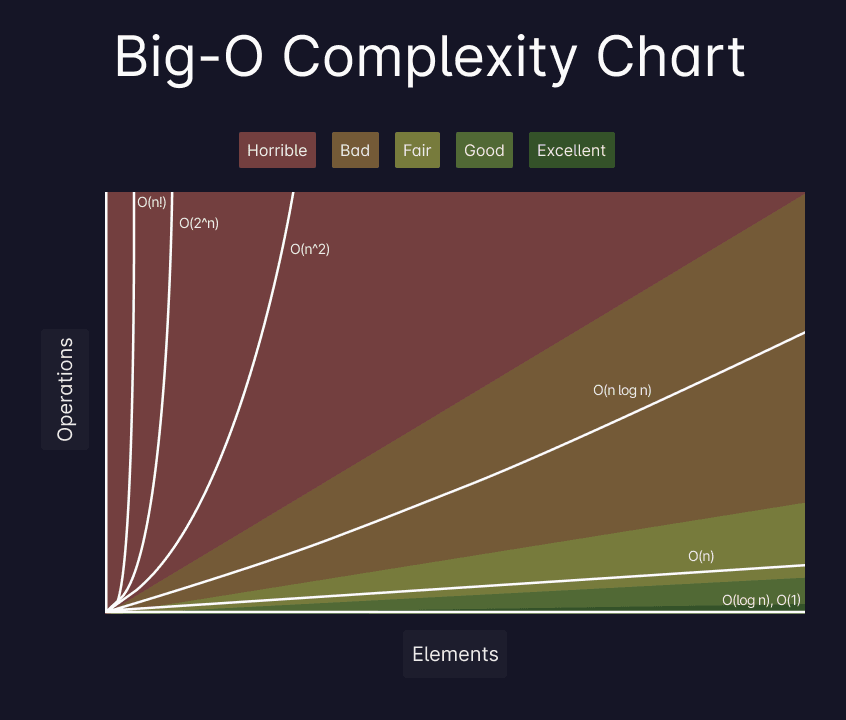
console.log(sortedArray);Big-O notation, represents an algorithm's worst-case complexity. It uses algebraic terms to describe the complexity of an algorithm, allowing you to measure its efficiency and performance.
Different data structures have different time complexities for the same operations. Below you can find average and worst time complexities for data structures used commonly in web development.
| Data Structure | Access | Search | Insertion | Deletion | Space Complexity |
|---------------------|----------|----------|-----------|-----------|------------------|
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) | Θ(n) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) | Θ(n) |
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) | Θ(n) |
| Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | Θ(n) |
| Doubly Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | Θ(n) |
| Skip List | Θ(log n) | Θ(log n) | Θ(log n) | Θ(log n) | O(n log(n)) |
| Hash Table | N/A | Θ(1) | Θ(1) | Θ(1) | Θ(n) |
| Binary Search Tree | Θ(log n) | Θ(log n) | Θ(log n) | Θ(log n) | Θ(n) || Data Structure | Access | Search | Insertion | Deletion | Space Complexity |
|--------------------|--------|--------|-----------|----------|------------------|
| Array | O(1) | O(n) | O(n) | O(n) | Θ(n) |
| Queue | O(n) | O(n) | O(1) | O(1) | Θ(n) |
| Stack | O(n) | O(n) | O(1) | O(1) | Θ(n) |
| Linked List | O(n) | O(n) | O(1) | O(1) | Θ(n) |
| Doubly Linked List | O(n) | O(n) | O(1) | O(1) | Θ(n) |
| Skip List | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | N/A | O(n) | O(n) | O(n) | Θ(n) |
| Binary Search Tree | O(n) | O(n) | O(n) | O(n) | Θ(n) |Similar to data structures, different array sorting algorithms have different time complexities. Below you can find the best, average and worst time complexities for the most common array sorting algorithms.
| Algorithm | Best | Average | Worst |
|----------------|------------|------------|------------|
| Quick sort | Ω(n log n) | Θ(n log n) | O(n^2) |
| Merge sort | Ω(n log n) | Θ(n log n) | O(n log n) |
| Heap sort | Ω(n log n) | Θ(n log n) | O(n log n) |
| Bubble sort | Ω(n) | Θ(n^2) | O(n^2) |
| Insertion sort | Ω(n) | Θ(n^2) | O(n^2) |
| Selection sort | Ω(n^2) | Θ(n^2) | O(n^2) |
| Bucket sort | Ω(n+k) | Θ(n+k) | O(n^ |- O(1): Constant time always takes the same time regardless of input size.
// Example: Accessing an array element by index.
function accessElement(arr, index) {
return arr[index];
}- O(log N): Logarithmic time as input size doubles, only one additional step is needed.
// Example: Binary search on a sorted array.
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
return mid;
}
if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}- O(N): Linear time time taken grows linearly with input size.
// Example: Looping through an array.
function findMax(arr) {
let max = arr[0];
for (const num of arr) {
if (num > max) {
max = num;
}
}
return max;
}- (N log N): N times log N time common in efficient sorting algorithms.
// Example: Merge sort.
function mergeSort(arr) {
if (arr.length <= 1) {
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
const result = [];
let i = 0;
let j = 0;
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
result.push(left[i]);
i++;
} else {
result.push(right[j]);
j++;
}
}
return result.concat(left.slice(i)).concat(right.slice(j));
}- O(N²): Quadratic time time grows with the square of input size.
// Example: Nested loops, such as in bubble sort.
function bubbleSort(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length - 1; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
return arr;
}- O(N³): Cubic time time grows with the cube of input size.
// Example: Triple nested loops, common in matrix multiplication.
function matrixMultiply(A, B) {
const rowsA = A.length;
const colsA = A[0].length;
const rowsB = B.length;
const colsB = B[0].length;
if (colsA !== rowsB) return null;
const C = new Array(rowsA).fill(0).map(() => new Array(colsB).fill(0));
for (let i = 0; i < rowsA; i++) {
for (let j = 0; j < colsB; j++) {
for (let k = 0; k < colsA; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return C;
}- O(2^N): Exponential time time grows exponentially with input size.
// Example: Recursive Fibonacci function.
function fib(n) {
if (n <= 1) {
return n;
}
return fib(n - 1) + fib(n - 2);
}- O(N!): Factorial time time grows with the factorial of input size.
// Example: Generating All Subsets of a Set
function generateSubsets(set) {
const result = [[]];
for (const item of set) {
const newSubsets = result.map(subset => [...subset, item]);
result.push(...newSubsets);
}
return result;
}
const set = [1, 2, 3];
console.log(generateSubsets(set));