-
Notifications
You must be signed in to change notification settings - Fork 416
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Generalize vorticity (and related functions) to allow for map projections #893
Comments
|
So while the docs for As far as the mapping/projection issues are concerned, that's still an open issue (covered in #174). So I'm a little unclear--is the map factor there to handle irregularly-spaced points or to handle issues from projection? or both? |
|
OK, I see that Regarding the map factors, they are fundamentally there to handle issues from projection. One of those issues is that the data array is irregularly spaced, but another issue is that computing vorticity (more generally, the curl of a vector) in a quantitatively correct manner requires the map factors. The current implementation of However, when the data is not truly Cartesian (e.g., NWP output on some map projection), the third and fourth terms above are necessary for a quantitatively correct calculation. In many (most?) instances, the third and fourth terms will be quite small, certainly not noticeable qualitatively (say, when looking at contours), but one case where the difference is noticeable is when vorticity is computed from data on a lat/lon grid and examined in polar regions (where, due to convergence of the meridians, the dmx/dy term gets large). For instance, compare the GEMPAK and MetPy-derived plots below (Python code is at https://gist.github.com/sgdecker/496f7ea7edd98b428ac3adab0b5e0842; GEMPAK is at https://gist.github.com/sgdecker/1a0bbf2e18dd0a2f9b4b02c83e07509b): A mathematical way to see this is to note that vorticity in spherical coordinates is given by (with theta as colatitude): The divergence and laplacian operators will have the same issue. |
|
Thanks for the detailed analysis. It's what I figured, and definitely on our roadmap. Due to the nicely detailed analysis, let's leave this open for addressing the map factors, and we can close out #174. (Putting the link to the NOAA writeup about map projections here: https://www.arl.noaa.gov/hysplit/cmapf-mapping-routines/) |
|
Nice resource in the ARL guide. I do want to suggest caution in retaining 3D coordinates as much as possible, as I advocated in the Cartopy PlateCaree saga - while the ARL guide has nice routines for 2D, and that's fine for maps, it can make forward/inverse and mixed-coordinate plotting difficult. Anyway, proj.4 has a 3D-aware forward / inverse, and a quick search turns up partial derivative support through the proj_factors function - maybe that's useful in ensuring we account for what @sgdecker points out above. This issue on OSGeo also seems related. |
|
I haven't tried implementing this yet, but I think the general solution would be to accept the data CRS object as an optional argument, rather than more specific things such as latitude. If that argument is not provided, assume the grid is Cartesian, and set the map factors to one. Otherwise, use the CRS object to obtain the map factors via proj4 (as discussed by @deeplycloudy). In either case, use the formula in my original comment as the basis for the computation. The part that is unclear to me without actually trying this yet is how difficult obtaining the map factors from the CRS is. |
|
This question is more related to the information needed for projection-aware deriviative-based calculations, rather than the implementation, but I still wanted to ask, since it may end up being useful for the implementation. I've recently been planning out a collection of "dataset helpers" to flesh out any missing CF metadata in xarray Datasets, so that all of the MetPy-xarray integration functionality (projections, coordinates, units, and hopefully soon variable identification and the field solver) works as smoothly as possible. WRF output has been the motivating example (see #1004). With that in mind, what would be the best set of information to standardize having in a DataArray and/or Dataset to ensure that these projection-aware calculations can be carried out? Is it sufficient to have
or am I missing something else? The goal, I would think, would be to be able to calculate something like vorticity with a call such as vorticity = mpcalc.vorticity(data['u_wind'], data['v_wind'])and have everything else be obtained automatically from the DataArrays. This, if combined with some way of annotating the function and its arguments, would also really set the stage for the field solver. |
|
Correct, my ideal is to have the CRS information, as well as coordinates like x or lon, attached to the data arrays. If we can't get map factors from the CRS...that would be bad. |
|
While I had hoped that #1260 (which allows for easy calculation of both nominal and actual grid deltas from a parsed DataArray) would be enough to make this feasible for quick implementation for v1.0, #1275 raised the point about grid-relative vs. earth-relative winds that I had not fully considered with respect to this issue. So,
With all this extra complexity, though, I unfortunately don't see a way that this can feasibly be resolved with a stable API for v1.0 in the immediate future. So, will this issue need to be punted from v1.0, and instead, for now, just use a simple xarray input/output wrapper that fills in the default grid spacing ( |
|
The equation way back in the first comment is valid for grid-relative |
|
@jthielen I agree about punting from 1.0. I'll do some milestone work later, but it's pretty clear we're not going to get the 1.0 we want, but the one we deserve. 😉 We can talk more when you get into AMS. Let me know. |
Sounds good. I'll be getting in tomorrow afternoon. We can chat via email if you want to find a more specific time, otherwise I'll plan on stopping by the Unidata table at the career fair that evening. |
|
This notebook from @deeplycloudy may help shed some light on using PyProj for some complicated reprojections. |
|
Okay, so I have compiled the vast majority of calculations affected by the spherical calculations. What this really all comes down to is whether we are doing a derivative on a vector quantity...so I have created a notebook that contains a vector_gradient function that computes the appropriate vector derivatives and then I use that throughout the notebook to calculate the various quantities. I've primarily focused on the GFS calculations since I had them all done for the comparisons to GEMPAK calculations. I have also included the vorticity calculation for the NAM projection, NAM Stereographic projection, and GFS stereographic projection. There is a slight nuance to calculating the grid dx and dy between the lat/lon grid of the GFS and the other projected grids, which is captured in the vector_gradient function. We can discuss potential implementation options on the next dev call. Notebook is hosted at: https://gist.github.com/kgoebber/b3546977e55fef96d4b36f4ef573a788 |
|
@kgoebber Question on the most recent notebook: In the dx and dy calculation for the latitude_longitude grid, you have earth_radius = 6371200 * units.meter
dx = 2*np.pi*earth_radius / u.lon.size
dy = -dxHowever, this looks to only be valid when assuming a spherical earth with radius 6371.2 km, longitude with global extent, and equal spacing in latitude and longitude. Would it be reasonable to generalize this to the following? geod = u.metpy.pyproj_crs.get_geod()
dx = units.Quantity(
geod.a * np.diff(u.metpy.longitude.metpy.unit_array.m_as('radian')),
'meter'
)
lat = u.metpy.latitude.metpy.unit_array.m_as('radian')
lon_meridian_diff = np.zeros(len(lat) - 1)
forward_az, _, dy = geod.inv(
lon_meridian_diff, lat[:-1], lon_meridian_diff, lat[1:], radians=True
)
dy[(forward_az < -90.) | (forward_az > 90.)] *= -1
dy = units.Quantity(dy, 'meter')Essentially, no matter what subset or spacing of longitudes and latitudes, this calculates the |
|
Ah yes, I have only been working with the global GFS, so the logic would break down for smaller subsets. A quick test of your generalization was good except for the dy were not negative as they needed to be. All forward azimuths were 3.1415926 (Pi because of 1 degree spacing?), so don't know if there is some different logic with the forward_az or just multiplying dy by -1 is best. I don't match the GEMPAK values as well, but that would be expected because we are not using the radius that they define. Despite that, it is different by only a very very small amount (what would be expected by using a different radius value. |
Yeah, not sure where that sign/direction error would be coming from. I'd be tempted to just reverse the directionality in the
Does specifying the matching ellipsoid fix it? I.e., replace gfs_data = xr.open_dataset('gfs_test_data.nc').metpy.parse_cf()with gfs_data = xr.open_dataset('gfs_test_data.nc').metpy.assign_crs({
'grid_mapping_name': 'latitude_longitude',
'earth_radius': 6371200
})Also, I hacked away at a possible implementation: jthielen@aac4e8e. Right now,
But, it's at least getting the ideas I had down in code, so if anyone wanted to take advantage of it as a head start towards an actual PR, go ahead! If not, I can try further iterating on it, but not sure when I'd be able to do so next. |
|
All checks out with the specific radius. Actually improves it marginally! |
|
@kgoebber Looks great! Thanks for putting all this together. It looks like there is some difference between the GEMPAK and MetPy PV calculations that isn't attributable to the map projection. Is that a known discrepancy (however minor it may be)? |
|
@dopplershift and I chat about this earlier today; I'm going to spin off @jthielen's commit above into a draft PR this week and begin the process of implementing it across functions, examining existing tests, and adding new tests. If you are already working on a PR, let me know! |
|
Not sure if this was the impression of other folks or not, but I previously conceptualized these map factor corrections as only occurring in derivatives on vector quantities. #2356 (comment) made me realize this does not seem to be the case; map factors need to be considered in any vector operation (so, also gradients of scalar fields, dot products, cross products, etc.). However, these corrections are much simpler (just coefficients on terms and they sometimes cancel out). |
|
I keep on getting nerd sniped with this topic of "vector calculus on orthogonal coordinates," and while I don't have much new to show for it yet, one particular concern came up: Do we need to delineate between vector component arguments that are scaled according to the covariant basis versus the normalized basis? (See https://en.wikipedia.org/wiki/Orthogonal_coordinates#Covariant_basis for discussion.) Is it safe to assume we will always have things in the normalized basis? |
For what it's worth, the Pielke textbook says (p. 129 of the second edition) "By convention, the equations [the set of equations solved in an NWP model] are written in the contravariant form, using the covariant differentiation operation..." but that is in the context of a whole bunch of derivations. I think in practice all of the vector quantities MetPy would be dealing with are normalized (e.g., if the u-component of the wind is given as 20 m/s, it really is 20 m/s at that point). |
|
On the topic of frequently having this problem in the back of my mind, I ended up writing up a rough proposal for addressing this "grid-correct vector calculus" problem on the data model level: pydata/xarray#6331. I doubt that all would be practical on the timeline we want to have this functionality implemented in MetPy, but, it could be a cool future goal? |
👍 to all of that |
|
Implemented in #2743. |








Some MetPy functions, such as gradient and advection, allow the user to supply arrays of deltas rather than a single value, but vorticity (and its relatives) does not. Vorticity is more complicated since derivatives of the "map factors" are also required, but it should be doable.
Here is the necessary computation according to the GEMPAK documentation (Appendix B2):
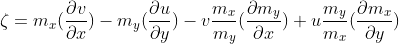
Since the map factors (m_x and m_y) are equivalent to the "nominal" grid spacing (\partial x and \partial y in the above equation) divided by the actual delta, an additional "nominal_delta" argument to vorticity would allow for the map factors to be computed. Since the WRF model provides the map factors in its output, allowing the map factors (and the nominal grid spacing) as optional arguments to vorticity in lieu of deltas would be useful as well.
The text was updated successfully, but these errors were encountered: