algo_math.md

Math algorithms

Namespace	Description
algo::math::discrete	Algorithms derived from discrete/combinatorial mathematics.
algo::math::random_num	Random numbers.
algo::math::random_num::cont	Random numbers using continuous probability distributions.
algo::math::random_num::discr	Random numbers using discrete probability distributions.
algo::math::prime	Prime numbers.

Discrete mathematics algorithms

Pascal's triangle

PTriangle PascalsTriangle(const unsigned int& depth);

Returns the first number of rows defined by depth of the Pascal's triangle. PTriangle is the same as std::vector<std::vector<int>>. Each item at row and column is computed as the binomial coefficient

The first six rows in the Pascal's triangle are:

Usage

#include <iostream>

#include "algo.hpp"

using namespace algo::math::discrete;
usign namespace std;

...

PTriangle rows{discrete::PascalsTriangle(5)};

for (const auto& row: rows) {
  for (const auto& k: row) {
    cout << k << " ";
  } 
  cout << endl;
}

Output:

> 1 
> 1 1 
> 1 2 1 
> 1 3 3 1 
> 1 4 6 4 1 
> 1 5 10 10 5 1 

Clock angle

int ClockAngle(const int &h, const int &m)

Reurns the angle between the hour and minute hands.

Knapsack problem, resource allocation

The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items. The problem often arises in resource allocation where the decision makers have to choose from a set of non-divisible projects or tasks under a fixed budget or time constraint, respectively. Wikipedia

int Knapsack(const Items& items, unsigned capacity);

Returns the maximum value that is possible to put in the knapsack without overloading the maximum capacity. The items hold the value and capacity for each item. Items is the same as std::vector<Item> and contains Item{int value, weight}.

Usage

#include "algo.hpp"

using namespace algo::math::discrete;

...

// Value, weight
Items items{{60, 10},
            {100, 20},
            {120, 30}};

int max_load{Knapsack(items, 50)}; // 220

The Euclidean algorithm

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. Wikipedia

With the properties of GCD, it can be used to compute the least common divisor, LCM:

The GCD and LCM functions are simple enough to be declared as constexpr lambdas:

constexpr auto GCD = [](auto a, auto b) {...};

constexpr auto LCM = [](auto a, auto b) {...};

Binomial coefficients

This function is also called choose . What the function is returning is the answer for the question "how many times can I choose different elements from a set of unique elements?"

It's calculated with

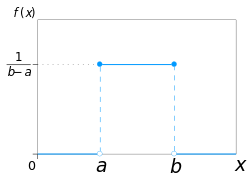
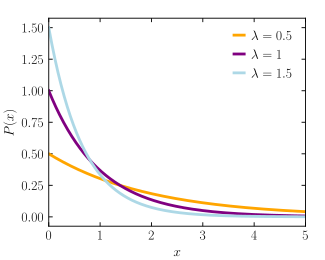
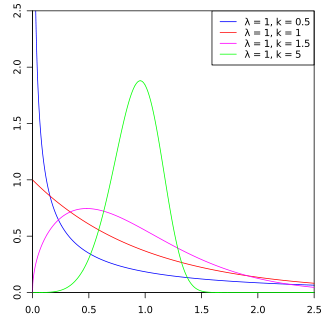
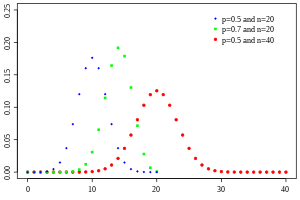
constexpr auto BIN = [](auto n, auto k) {...};

Retuns the result of .

Random numbers

Images below kindly borrowed from Wikipedia.

Function	Properties	PDF (continuous) / PMF (discrete)
double cont::Uniform(const double& a, const double& b);
double cont::Random();	Uniform(0, 1)
double cont::Exp(const double& lambda);
double cont::Normal(const double& mu, const double& sigma);
double cont::Weibull(const double& lambda, const double& k);
int discr::Binomial(const int& n, const double& p);
int discr::Poisson(const double& lambda);
int discr::Geometric(const double& p);

Prime numbers

Sieve of Eratosthenes

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. Wikipedia

std::vector<T> GetPrimes(unsigned int n);

Returns a list of prime numbers where the last prime number is <= n.

To verify that an integer is a prime number use this function;

bool IsPrime(T n);