https://leetcode.cn/problems/find-the-number-of-ways-to-place-people-ii/
给你一个 n x 2 的二维数组 points ,它表示二维平面上的一些点坐标,其中 points[i] = [xi, yi] 。
我们定义 x 轴的正方向为 右 (x 轴递增的方向),x 轴的负方向为 左 (x 轴递减的方向)。类似的,我们定义 y 轴的正方向为 上 (y 轴递增的方向),y 轴的负方向为 下 (y 轴递减的方向)。
你需要安排这 n 个人的站位,这 n 个人中包括 Alice 和 Bob 。你需要确保每个点处 恰好 有 一个 人。同时,Alice 想跟 Bob 单独玩耍,所以 Alice 会以 Bob 的坐标为 左上角 ,Bob 的坐标为 右下角 建立一个矩形的围栏(注意,围栏可能 不 包含任何区域,也就是说围栏可能是一条线段)。如果围栏的 内部 或者 边缘 上有任何其他人,Alice 都会难过。
请你在确保 Alice 不会 难过的前提下,返回 Alice 和 Bob 可以选择的 点对 数目。
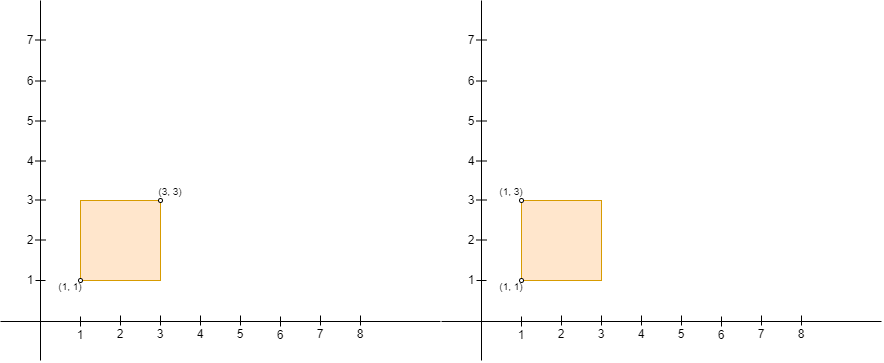
注意,Alice 建立的围栏必须确保 Alice 的位置是矩形的左上角,Bob 的位置是矩形的右下角。比方说,以 (1, 1) ,(1, 3) ,(3, 1) 和 (3, 3) 为矩形的四个角,给定下图的两个输入,Alice 都不能建立围栏,原因如下:
- 图一中,Alice 在
(3, 3)且 Bob 在(1, 1),Alice 的位置不是左上角且 Bob 的位置不是右下角。 - 图二中,Alice 在
(1, 3)且 Bob 在(1, 1),Bob 的位置不是在围栏的右下角。
示例 1:
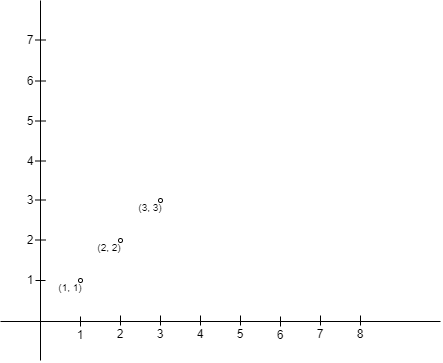
输入:points = [[1,1],[2,2],[3,3]] 输出:0 解释:没有办法可以让 Alice 的围栏以 Alice 的位置为左上角且 Bob 的位置为右下角。所以我们返回 0 。
示例 2:
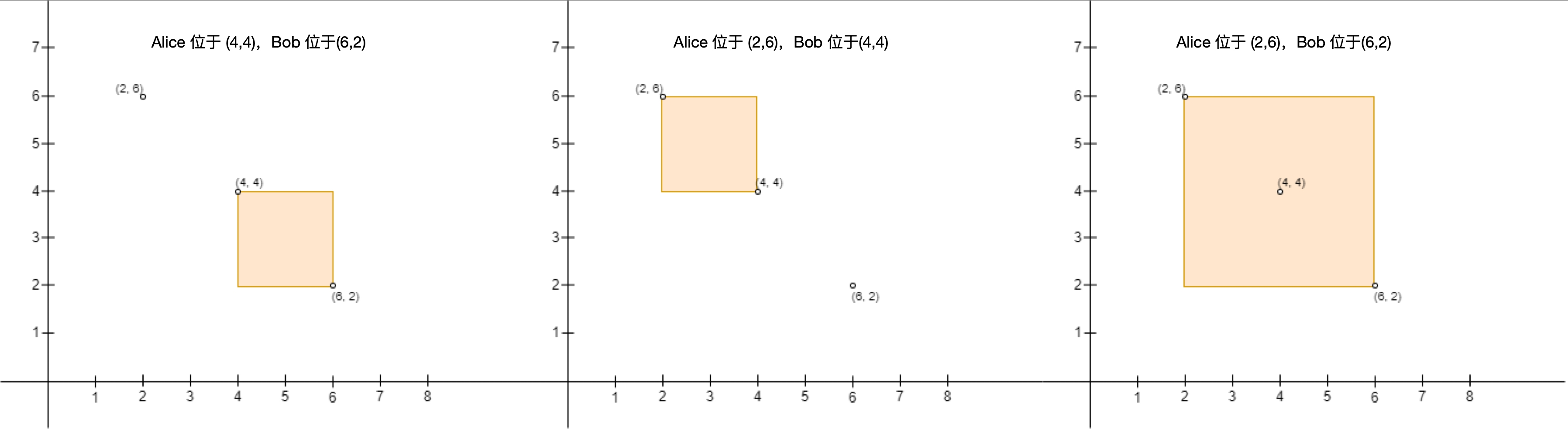
输入:points = [[6,2],[4,4],[2,6]] 输出:2 解释:总共有 2 种方案安排 Alice 和 Bob 的位置,使得 Alice 不会难过: - Alice 站在 (4, 4) ,Bob 站在 (6, 2) 。 - Alice 站在 (2, 6) ,Bob 站在 (4, 4) 。 不能安排 Alice 站在 (2, 6) 且 Bob 站在 (6, 2) ,因为站在 (4, 4) 的人处于围栏内。
示例 3:
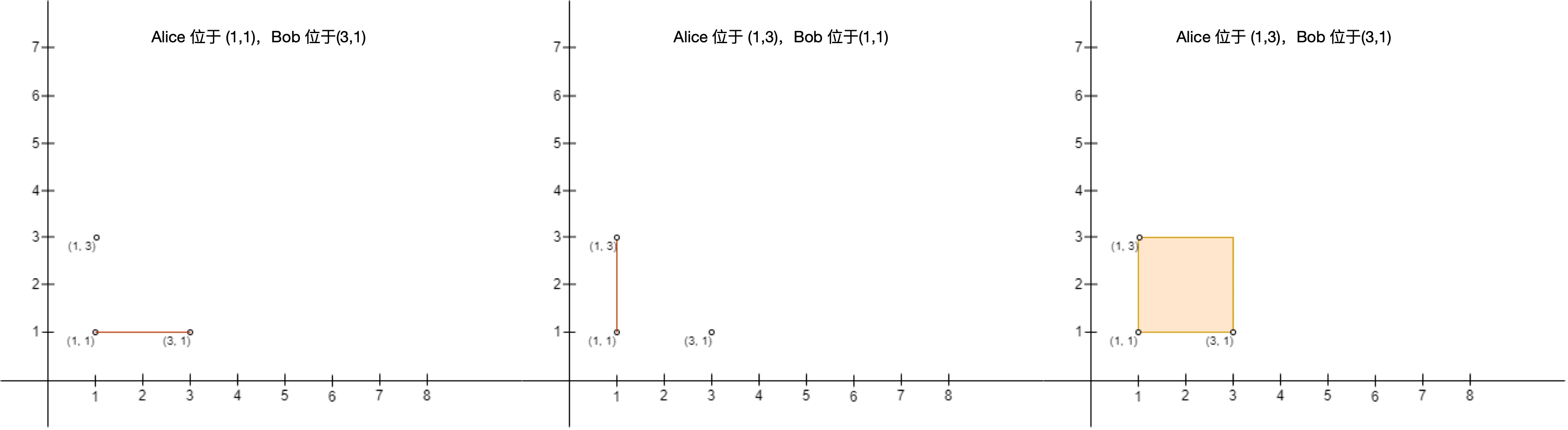
输入:points = [[3,1],[1,3],[1,1]] 输出:2 解释:总共有 2 种方案安排 Alice 和 Bob 的位置,使得 Alice 不会难过: - Alice 站在 (1, 1) ,Bob 站在 (3, 1) 。 - Alice 站在 (1, 3) ,Bob 站在 (1, 1) 。 不能安排 Alice 站在 (1, 3) 且 Bob 站在 (3, 1) ,因为站在 (1, 1) 的人处于围栏内。 注意围栏是可以不包含任何面积的,上图中第一和第二个围栏都是合法的。
提示:
2 <= n <= 1000points[i].length == 2-109 <= points[i][0], points[i][1] <= 109points[i]点对两两不同。
- 暂无
- 暂无
为了方便确定谁是 alice,谁是 bob,首先我们按 x 正序排序。
令索引 i 是 alice (x1, y1),索引 j != i 的都可能作为 bob(x2, y2)。那什么样的 j 满足条件呢?需要满足:
-
alice 纵坐标要大于等于 bob(横坐标由于排序已经保证了 alice 不大于 bob,满足题目要求)
-
中间的点纵坐标要么比两人都大,要么比两人都小。(即中间的点的纵坐标不能位于 alice 和 bob 中间)
有一个特殊的 case: alice 和 bob 的横坐标相等,这种情况下如果 i 的纵坐标小于 j 的纵坐标,不一定是不满足题意的。因此 alice 和 bob 横坐标相等,因此我们可以将 alice 看成是 bob, bob 看成是 alice。经过这样的处理,就又满足题意了。
为了不做这种特殊处理,我们可以按照 x 正序排序的同时,对 x 相同的按照 y 逆序排序,这样就不可能出现横坐标相同,i 的纵坐标小于 j 的纵坐标的情况。另外这样在 i 确定的时候,i 前面的点也一定不是 j,因此只需要枚举 i 之后的点即可。
这样会错过一些情况吗?不会!因为这种 case 会在其他遍历的时候中枚举到。
因此我们可以枚举 i 为 alice, j > i 为 bob。然后枚举 i 个 j 中间的点是否满足题意(不在 i 和 j 中间的不用看)。
接下来,我们看如何满足前面提到的两点。
对于第一点,只需比较 alice 和 bob 的 y 即可。
对于第二点,我们只需要记录最大的 y 即可。只要 y2 大于最大的 y 就行。如果 y2 <= max <= y1,那么就不行,否则可以。 其中 max 是 最可能在 alice 和 bob 之间的 y,这样不需要全部比较。这个所谓最可能得就是最大的 y。
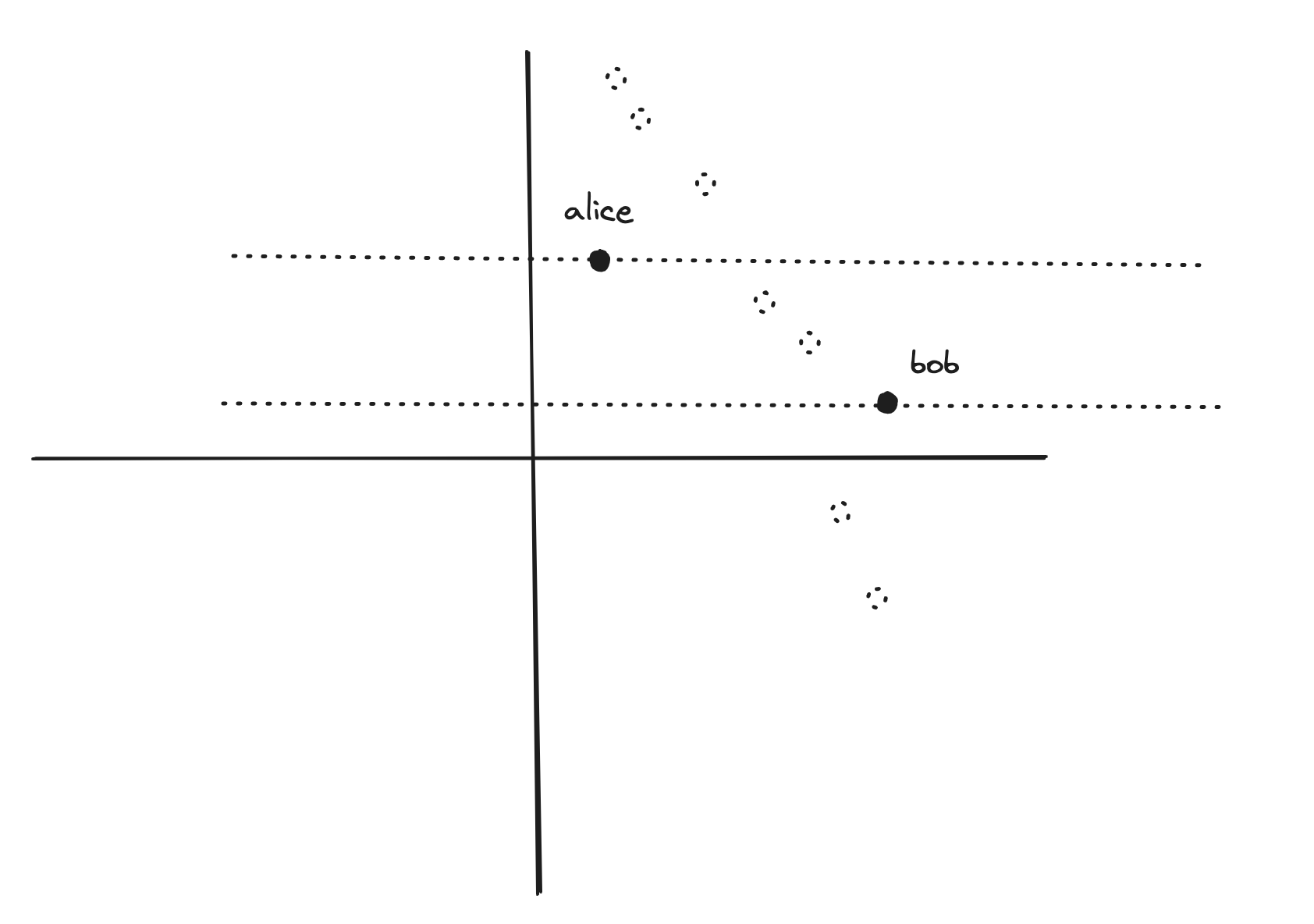
大家可以结合图来理解。
如图,虚点是 i 和 j 中间的点。对于这些点只要纵坐标不在图上的两个横线之间就行。因此这些点的纵坐标都要么大于 y1,要么小于 y2。换句话说,这些点的纵坐标要么最小值大于 y1,要么最大值小于 y2。因此我们只需要记录最大的 y 即可。
- 排序
- 语言支持:Python3
Python3 Code:
class Solution:
def numberOfPairs(self, points: List[List[int]]) -> int:
points.sort(key=lambda p: (p[0], -p[1]))
ans = 0
for i, (x1, y1) in enumerate(points): # point i
max_y = -inf
min_y = inf
for (x2, y2) in points[i + 1:]: # point j
if y1 < y2: continue # 确保条件1
if y2 > max_y or y1 < min_y: # 确保条件2
ans += 1
max_y = max(max_y, y2)
min_y = min(min_y, y2)
return ans复杂度分析
令 n 为 points 长度。
- 时间复杂度:$O(nlogn)$
- 空间复杂度:$O(1)$
此题解由 力扣刷题插件 自动生成。
力扣的小伙伴可以关注我,这样就会第一时间收到我的动态啦~
以上就是本文的全部内容了。大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 40K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。
关注公众号力扣加加,努力用清晰直白的语言还原解题思路,并且有大量图解,手把手教你识别套路,高效刷题。