https://leetcode-cn.com/problems/zuma-game/
回忆一下祖玛游戏。现在桌上有一串球,颜色有红色(R),黄色(Y),蓝色(B),绿色(G),还有白色(W)。 现在你手里也有几个球。
每一次,你可以从手里的球选一个,然后把这个球插入到一串球中的某个位置上(包括最左端,最右端)。接着,如果有出现三个或者三个以上颜色相同的球相连的话,就把它们移除掉。重复这一步骤直到桌上所有的球都被移除。
找到插入并可以移除掉桌上所有球所需的最少的球数。如果不能移除桌上所有的球,输出 -1 。
示例:
输入: "WRRBBW", "RB"
输出: -1
解释: WRRBBW -> WRR[R]BBW -> WBBW -> WBB[B]W -> WW (翻译者标注:手上球已经用完,桌上还剩两个球无法消除,返回-1)
输入: "WWRRBBWW", "WRBRW"
输出: 2
解释: WWRRBBWW -> WWRR[R]BBWW -> WWBBWW -> WWBB[B]WW -> WWWW -> empty
输入:"G", "GGGGG"
输出: 2
解释: G -> G[G] -> GG[G] -> empty
输入: "RBYYBBRRB", "YRBGB"
输出: 3
解释: RBYYBBRRB -> RBYY[Y]BBRRB -> RBBBRRB -> RRRB -> B -> B[B] -> BB[B] -> empty
标注:
你可以假设桌上一开始的球中,不会有三个及三个以上颜色相同且连着的球。
桌上的球不会超过20个,输入的数据中代表这些球的字符串的名字是 "board" 。
你手中的球不会超过5个,输入的数据中代表这些球的字符串的名字是 "hand"。
输入的两个字符串均为非空字符串,且只包含字符 'R','Y','B','G','W'。
- 回溯
- 哈希表
- 双指针
- 百度
面试题困难难度的题目常见的题型有:
- DP
- 设计题
- 图
- 游戏
本题就是游戏类题目。 如果你是一个前端, 说不定还会考察你如何实现一个 zuma 游戏。这种游戏类的题目,可以简单可以困难, 比如力扣经典的石子游戏,宝石游戏等。这类题目没有固定的解法。我做这种题目的思路就是先暴力模拟,再尝试优化算法瓶颈。
注意下数据范围球的数目 <= 5,因此暴力法就变得可行。基本思路是暴力枚举手上的球可以消除的地方, 我们可以使用回溯法来完成暴力枚举的过程,在回溯过程记录最小值即可。由于回溯树的深度不会超过 5,因此这种解法应该可以 AC。
上面提到的可以消除的地方,指的是连续相同颜色 + 手上相同颜色的球大于等于 3,这也是题目说明的消除条件。
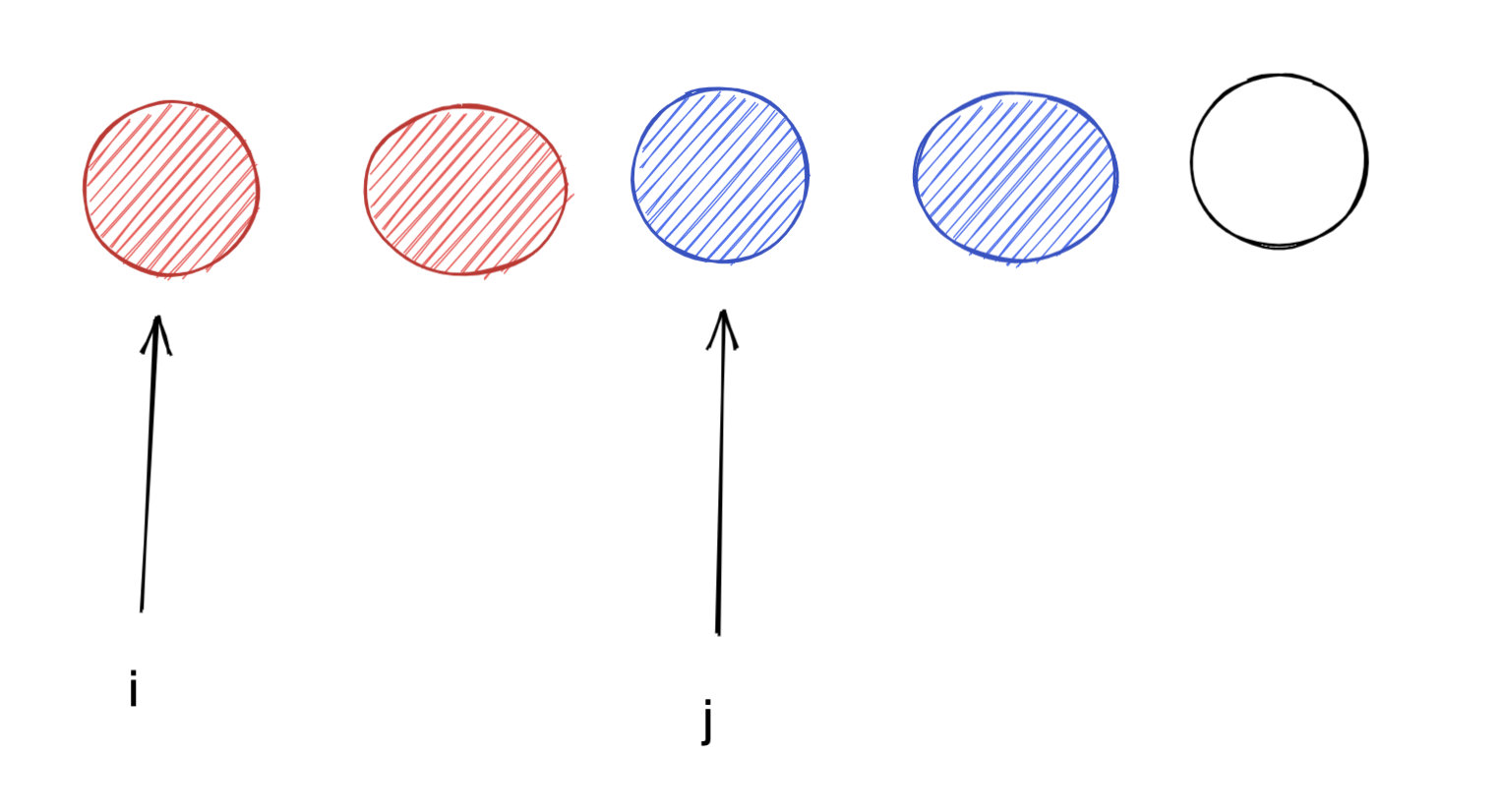
因此我们只需要两个指针记录连续相同颜色球的位置,如果可以消除,消除即可。
如图,我们记录了连续红球的位置, 如果手上有红球, 则可以尝试将其清除,这一次决策就是回溯树(决策树)的一个分支。之后我们会撤回到这个决策分支, 尝试其他可行的决策分支。
以 board = RRBBRR , hand 为 RRBB 为例,其决策树为:
其中虚线表示无需手动干预,系统自动消除。叶子节点末尾的黄色表示全部消除需要的手球个数。路径上的文字后面的数字表示此次消除需要的手球个数
如果你对回溯不熟悉,可以参考下我之前写的几篇题解:比如 46.permutations。
可以看出, 如果选择先消除中间的蓝色,则只需要一步即可完成。
关于计算连续球位置的核心代码(Python3):
i = 0
while i < len(board):
j = i + 1
while j < len(board) and board[i] == board[j]: j += 1
# 其他逻辑
# 更新左指针
i = j具体算法:
-
用哈希表存储手上的球的种类和个数,这么做是为了后面快速判断连续的球是否可以被消除。由于题目限制手上求不会超过 5,因此哈希表的最大容量就是 5,可以认为这是一个常数的空间。
-
回溯。
2.1 确认可以消除的位置,算法参考上面的代码。
2.2 判断手上是否有足够相同颜色的球可以消除。
2.3 回溯的过程记录全局最小值。
- 回溯模板
- 双指针写法
代码支持:Python3
Python3 Code:
class Solution:
def findMinStep(self, board: str, hand: str) -> int:
def backtrack(board):
if not board: return 0
i = 0
ans = 6
while i < len(board):
j = i + 1
while j < len(board) and board[i] == board[j]: j += 1
balls = 3 - (j - i)
if counter[board[i]] >= balls:
balls = max(0, balls)
counter[board[i]] -= balls
ans = min(ans, balls + backtrack(board[:i] + board[j:]))
counter[board[i]] += balls
i = j
return ans
counter = collections.Counter(hand)
ans = backtrack(board)
return -1 if ans > 5 else ans复杂度分析
- 时间复杂度:$O(2^(min(C, 5)))$,其中 C 为连续相同颜色球的次数,比如 WWRRRR, C 就是 2, WRBDD, C 就是 4。min(C, 5) 是因为题目限定了手上球的个数不大于 5。
- 空间复杂度:$O(min(C, 5) * Board)$,其中 C 为连续相同颜色球的次数,Board 为 Board 的长度。
大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 36K star 啦。 大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。