https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
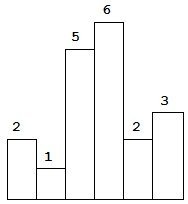
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
�
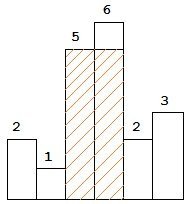
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入:[2,1,5,6,2,3]
输出:10
- 阿里
- 腾讯
- 百度
- 字节
- 单调栈
我们暴力尝试所有可能的矩形。由于矩阵是二维图形, 我我们可以使用左右两个端点来唯一确认一个矩阵。因此我们使用双层循环枚举所有的可能性即可。 而矩形的面积等于(右端点坐标 - 左端点坐标 + 1) * 最小的高度,最小的高度我们可以在遍历的时候顺便求出。
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n, ans = len(heights), 0
if n != 0:
ans = heights[0]
for i in range(n):
height = heights[i]
for j in range(i, n):
height = min(height, heights[j])
ans = max(ans, (j - i + 1) * height)
return ans复杂度分析
- 时间复杂度:$O(N^2)$
- 空间复杂度:$O(1)$
我们仍然暴力尝试所有可能的矩形。只不过我们这一次从中心向两边进行扩展。对于每一个 i,我们计算出其左边第一个高度小于它的索引 p,同样地,计算出右边第一个高度小于它的索引 q。那么以 i 为最低点能够构成的面积就是(q - p - 1) * heights[i]。 这种算法毫无疑问也是正确的。 我们证明一下,假设 f(i) 表示求以 i 为最低点的情况下,所能形成的最大矩阵面积。那么原问题转化为max(f(0), f(1), f(2), ..., f(n - 1))。
具体算法如下:
- 我们使用 l 和 r 数组。l[i] 表示 左边第一个高度小于它的索引,r[i] 表示 右边第一个高度小于它的索引。
- 我们从前往后求出 l,再从后往前计算出 r。
- 再次遍历求出所有的可能面积,并取出最大的。
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n = len(heights)
l, r, ans = [-1] * n, [n] * n, 0
for i in range(1, n):
j = i - 1
while j >= 0 and heights[j] >= heights[i]:
j -= 1
l[i] = j
for i in range(n - 2, -1, -1):
j = i + 1
while j < n and heights[j] >= heights[i]:
j += 1
r[i] = j
for i in range(n):
ans = max(ans, heights[i] * (r[i] - l[i] - 1))
return ans复杂度分析
- 时间复杂度:$O(N^2)$
- 空间复杂度:$O(N)$
实际上我们内层循环没必要一步一步移动,我们可以直接将j -= 1 改成 j = l[j], j += 1 改成 j = r[j]。
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n = len(heights)
l, r, ans = [-1] * n, [n] * n, 0
for i in range(1, n):
j = i - 1
while j >= 0 and heights[j] >= heights[i]:
j = l[j]
l[i] = j
for i in range(n - 2, -1, -1):
j = i + 1
while j < n and heights[j] >= heights[i]:
j = r[j]
r[i] = j
for i in range(n):
ans = max(ans, heights[i] * (r[i] - l[i] - 1))
return ans复杂度分析
- 时间复杂度:$O(N)$
- 空间复杂度:$O(N)$
实际上,读完第二种方法的时候,你应该注意到了。我们的核心是求左边第一个比 i 小的和右边第一个比 i 小的。 如果你熟悉单调栈的话,那么应该会想到这是非常适合使用单调栈来处理的场景。
从左到右遍历柱子,对于每一个柱子,我们想找到第一个高度小于它的柱子,那么我们就可以使用一个单调递减栈来实现。 如果柱子大于栈顶的柱子,那么说明不是我们要找的柱子,我们把它塞进去继续遍历,如果比栈顶小,那么我们就找到了第一个小于的柱子。 对于栈顶元素,其右边第一个小于它的就是当前遍历到的柱子,左边第一个小于它的就是栈中下一个要被弹出的元素,因此以当前栈顶为最小柱子的面积为当前栈顶的柱子高度 * (当前遍历到的柱子索引 - 1 - (栈中下一个要被弹出的元素索引 + 1) + 1),化简一下就是 当前栈顶的柱子高度 * (当前遍历到的柱子索引 - 栈中下一个要被弹出的元素索引 - 1)。
这种方法只需要遍历一次,并用一个栈。由于每一个元素最多进栈出栈一次,因此时间和空间复杂度都是$O(N)$。
为了统一算法逻辑,减少边界处理,我在 heights 首尾添加了两个哨兵元素,这样我们可以保证所有的柱子都会出栈。
代码支持: Python,CPP
Python Code:
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n, heights, st, ans = len(heights), [0] + heights + [0], [], 0
for i in range(n + 2):
while st and heights[st[-1]] > heights[i]:
ans = max(ans, heights[st.pop(-1)] * (i - st[-1] - 1))
st.append(i)
return ansCPP Code:
class Solution {
public:
int largestRectangleArea(vector<int>& A) {
A.push_back(0);
int N = A.size(), ans = 0;
stack<int> s;
for (int i = 0; i < N; ++i) {
while (s.size() && A[s.top()] >= A[i]) {
int h = A[s.top()];
s.pop();
int j = s.size() ? s.top() : -1;
ans = max(ans, h * (i - j - 1));
}
s.push(i);
}
return ans;
}
};复杂度分析
- 时间复杂度:$O(N)$
- 空间复杂度:$O(N)$
2020-05-30 更新:
有的观众反应看不懂为啥需要两个哨兵。 其实末尾的哨兵就是为了将栈清空,防止遍历完成栈中还有没参与运算的数据。
而前面的哨兵有什么用呢? 我这里把上面代码进行了拆解:
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n, heights, st, ans = len(heights),[0] + heights + [0], [], 0
for i in range(n + 2):
while st and heights[st[-1]] > heights[i]:
a = heights[st[-1]]
st.pop()
# 如果没有前面的哨兵,这里的 st[-1] 可能会越界。
ans = max(ans, a * (i - 1 - st[-1]))
st.append(i)
return ans大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。
大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。