- 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘입니다. 효율적인 정렬은 탐색이나 병합 알고리즘처럼 (정렬된 리스트에서 바르게 동작하는) 다른 알고리즘을 최적화하는 데 중요하며 데이터의 정규화나 의미있는 결과물을 생성하는 데 유용히 쓰입니다.
버블 정렬(Bubble sort)
-
서로 인접한 두 원소를 검사하여 정렬하는 알고리즘입니다.
-
인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환합니다.
-
과정
- 첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬합니다.
- 1회전을 수행하고 나면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료는 정렬에서 제외됩니다. 2회전을 수행하고 나면 끝에서 두 번째 자료까지는 정렬에서 제외됩니다.
- 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어납니다.
-
배열에 7, 4, 5, 1, 3이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬하는 과정은 아래와 같습니다.
버블 정렬(bubble sort) 알고리즘의 특징
-
장점
- 구현이 매우 간단합니다.
-
단점
- 순서에 맞지 않은 요소를 인접한 요소와 교환합니다.
- 하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열에서 모든 다른 요소들과 교환되어야 합니다. 특히 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어납니다.
- 일반적으로 자료의 교환 작업(SWAP)이 자료의 이동 작업(MOVE)보다 더 복잡하기 때문에 버블 정렬은 단순성에도 불구하고 거의 쓰이지 않습니다.
-
시간복잡도
- 비교 횟수
- 정렬이 돼있던 안돼있던, 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일합니다. 따라서 최상, 평균, 최악 모두 일정합니다.
- n-1, n-2, … , 2, 1 번 = n(n-1)/2
- 교환 횟수
- 입력 자료가 역순으로 정렬되어 있는 최악의 경우, 한 번 교환하기 위하여 3번의 이동(SWAP 함수의 작업)이 필요하므로 (비교 횟수 * 3) 번 = 3n(n-1)/2
- 입력 자료가 이미 정렬되어 있는 최상의 경우, 자료의 이동이 발생하지 않습니다.
- T(n) = O(n^2)
- 비교 횟수
선택 정렬 (Selection Sort)
-
원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘입니다.
- 첫 번째 순서에는 첫 번째 위치에 가장 최솟값을 넣습니다.
- 두 번째 순서에는 두 번째 위치에 남은 값 중에서의 최솟값을 넣습니다. ....
-
과정
-
- 주어진 배열 중에서 최솟값을 찾습니다.
-
- 그 값을 맨 앞에 위치한 값과 교체합니다.(패스(pass))
-
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체합니다.
-
- 하나의 원소만 남을 때까지 위의 1~3 과정을 반복합니다.
-
선택 정렬(selection sort) 알고리즘의 특징
-
장점
- 자료 이동 횟수가 미리 결정됩니다.
-
단점
- 안정성을 만족하지 않습니다.
- k+1 번째에 들어갈 요소를 찾기 위해 나머지 요소를 모두 탐색해야 합니다. (이에 반해 Insertion sort는 k+1 요소 배치에 필요한 만큼의 요소만 탐색하고 끝납니다. )
-
시간복잡도
- 비교 횟수
- 두 개의 for 루프의 실행 횟수
- 외부 루프: (n-1)번
- 내부 루프(최솟값 찾기): n-1, n-2, … , 2, 1 번
- 교환 횟수
- 외부 루프의 실행 횟수와 동일. 즉, 상수 시간 작업
- 한 번 교환하기 위하여 3번의 이동(SWAP 함수의 작업)이 필요하므로 3(n-1)번
- T(n) = (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)
- 비교 횟수
(Insertion Sort)
-
이미 정렬된 앞의 요소들 가운데서 내가 들어갈 자리를 찾아, 그 자리에 나 자신을 삽입하는 방식입니다.
-
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교 하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘입니다.
-
매 순서마다 해당 원소를 삽입할 수 있는 위치를 찾아 해당 위치에 넣습니다.
-
삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘입니다.
- 처음 Key 값은 두 번째 자료부터 시작합니다.
삽입 정렬 (Insertion Sort) 알고리즘의 특징
-
장점
- 안정성을 만족합니다.
- 레코드의 수가 적을 경우 알고리즘 자체가 매우 간단하므로 다른 복잡한 정렬 방법보다 유리합니다.
- 레코드가 이미 정렬되어 있는 경우에 매우 효율적입니다. (O(N))
-
단점
- 비교적 많은 레코드들의 이동을 포함합니다.
- 레코드 수가 많고 레코드 크기가 클 경우에 적합하지 않습니다.
-
시간복잡도
< 최선의 경우 >
- 비교 횟수
- 이동 없이 1번의 비교만 이루어진다.
- 외부 루프: (n-1)번
- Best T(n) = O(n)
< 최악의 경우(입력 자료가 역순일 경우) >
- 비교 횟수
- 외부 루프 안의 각 반복마다 i번의 비교 수행
- 외부 루프: (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)
- 교환 횟수
- 외부 루프의 각 단계마다 (i+2)번의 이동 발생
- n(n-1)/2 + 2(n-1) = (n^2+3n-4)/2 = O(n^2)
- Worst T(n) = O(n^2)
버블 정렬, 삽입 정렬, 삽입 정렬의 비교
| Bubble | Selection | Insertion | |
|---|---|---|---|
| 평균 | O(N^2) | O(N^2) | O(N^2) |
| 정렬 | O(N^2) | O(N^2) | O(N) |
-
Bubble VS Selection
- Bubble : 매번 swap 진행합니다.
- Selection : 비교하다가 한 번만 swap 합니다.
-
Selection VS Insertion
- Selection : k+1에 들어갈 요소 찾고자 모든 원소를 탐색/비교합니다.
- Insertion : k+1번째 원소가 자신의 앞에 이미 정렬된 배열에서 자신이 들어갈 자리를 찾을 때, 자신보다 작은 애를 만나면 탐색/비교를 멈춥니다.
퀵 정렬 (Quick Sort)
- 과정
-
- 리스트 안에 있는 한 요소를 선택합니다. 이렇게 고른 원소를 피벗(pivot) 이라고 합니다.
-
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨집니다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
-
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬합니다.
- 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복합니다.
- 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복합니다.
-
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복합니다.
-
- 리스트의 크기가 0이나 1이 될 때까지 반복합니다.
- 분할(Divide)
- 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할합니다.
- 정복(Conquer)
- 부분 배열을 정렬합니다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용합니다.
- 결합(Combine)
- 정렬된 부분 배열들을 하나의 배열에 합병합니다. 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있습니다.
퀵 정렬(quick sort) 알고리즘의 특징
- 장점
- 속도가 빠릅니다.
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠릅니다.
- 추가 메모리 공간을 필요로 하지 않습니다.
- O(log n)만큼의 메모리를 필요로 합니다.
- 단점
- 정렬된 리스트에 대해서는 퀵 정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸립니다.
- 퀵 정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택합니다.
- EX) 리스트 내의 몇 개의 데이터 중에서 크기순으로 중간 값(medium)을 피벗으로 선택합니다.
퀵 정렬(quick sort)의 시간복잡도
- 최선의 경우 : T(n) = O(nlog₂n)
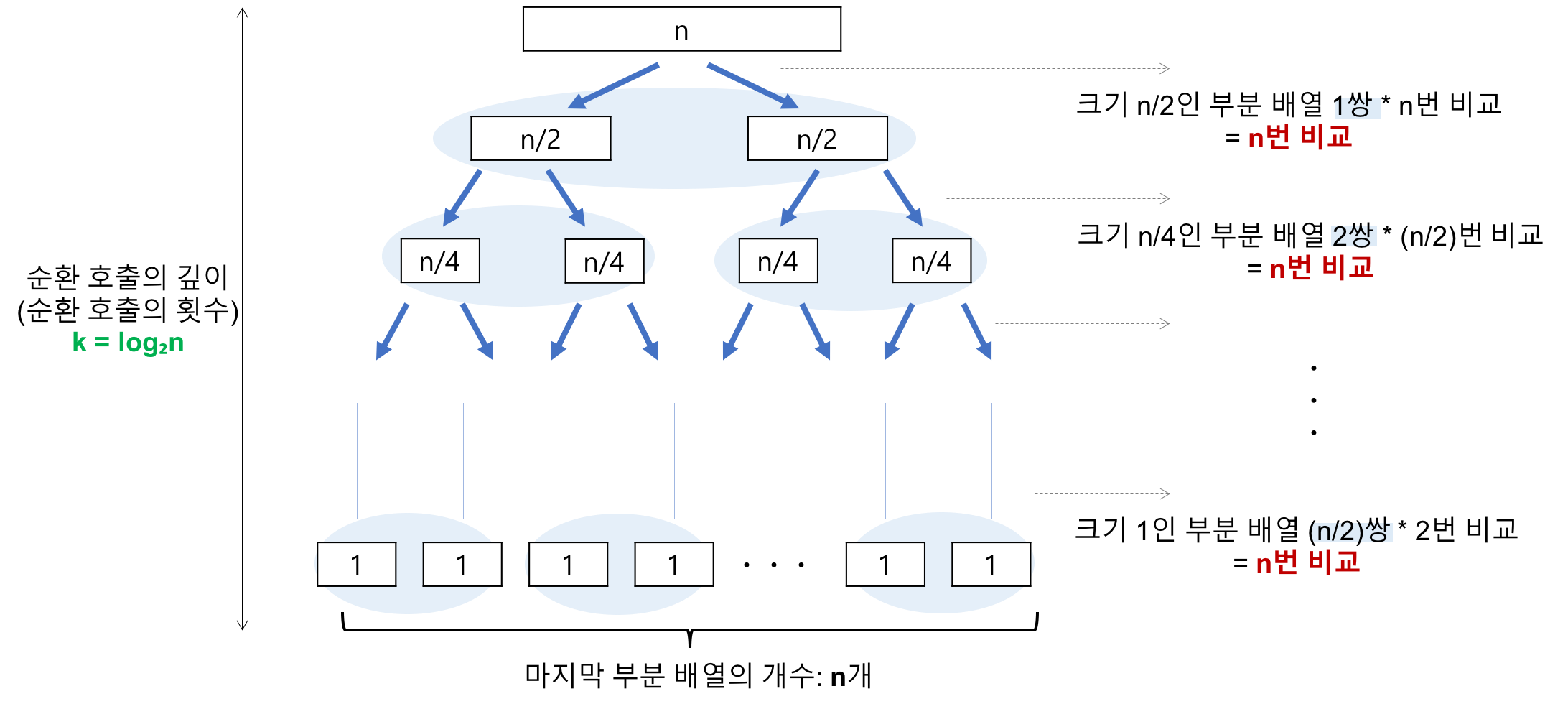 - 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)입니다.
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다. 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n
- 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)입니다.
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다. 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n
- 최악의 경우 : T(n) = O(n^2)
- 평균 : T(n) = O(nlog₂n)
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠릅니다. 퀵 정렬이 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문입니다.
병합 정렬 (Merge Sort)
-
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법입니다.
-
과정
-
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 간주합니다. 그렇지 않은 경우에는
-
- 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눕니다.
-
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬합니다.
-
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병합니다.
-
분할(Divide)
- 입력 배열을 같은 크기의 2개의 부분 배열로 분할합니다.
-
정복(Conquer)
- 부분 배열을 정렬합니다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용합니다.
-
결합(Combine)
- 정렬된 부분 배열들을 하나의 배열에 합병합니다.
-
합병 정렬의 구체적 과정
- 추가적인 리스트가 필요합니다.
- 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용합니다.
- 합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계입니다.
-
합병 정렬(merge sort) 알고리즘의 예제
- 배열에 27, 10, 12, 20, 25, 13, 15, 22이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬합니다.
- 2개의 정렬된 리스트를 합병(merge)하는 과정
-
- 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮깁니다.
-
- 둘 중에서 하나가 끝날 때까지 이 과정을 되풀이합니다.
-
- 만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사합니다.
-
- 새로운 리스트(sorted)를 원래의 리스트(list)로 옮깁니다.
-
합병 정렬 (Heap Sort) 알고리즘의 예제 그림
합병 정렬(merge sort) 알고리즘의 특징
- 단점
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요합니다.
- 제자리 정렬(in-place sorting)이 아닙니다.
- 레크드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래합니다.
- 장점
- 안정적인 정렬 방법입니다.
- 데이터의 분포에 영향을 덜 받습니다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일합니다. (O(NlogN)로 동일)
- 만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아집니다.
- 제자리 정렬(in-place sorting)로 구현할 수 있습니다.
- 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적입니다.
힙 정렬 (Heap Sort)
- 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법입니다.
- 내림차순 정렬을 위해서는 최대 힙을 구성합니다.
- 오름차순 정렬을 위해서는 최소 힙을 구성하면 됩니다.
- 최댓값과 최솟값을 찾는데 최적화되어있는 이유는 heap의 특성상 최대 힙일 때는 가장 큰 값이 루트 노드로 오게 되고 최소 힙일 때는 가장 작은 값이 루트 노드로 오기 때문입니다.
과정 설명
- 정렬해야 할 n개의 요소들로 최대 힙(완전 이진 트리 형태)을 만듭니다.
- 내림차순을 기준으로 정렬합니다.
- 그 다음으로 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장하면 됩니다.
- 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 됩니다.
힙 정렬(heap sort) 알고리즘의 특징
-
장점
- 시간 복잡도가 좋습니다.
- 힙 정렬이 유용한 경우는 전체 자료를 정렬하는 것이 아닌 가장 큰 값 몇개만 필요할 때입니다.
-
시간복잡도
- 힙 트리의 전체 높이가 거의 log₂n(완전 이진 트리이므로)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 log₂n만큼 소요된다.
- 요소의 개수가 n개 이므로 전체적으로 O(nlog₂n)의 시간이 걸린다.
- T(n) = O(nlog₂n)
기수 정렬 (Radix/Bucket Sort)
내용 출처 : https://lktprogrammer.tistory.com/48 사진 출처 : 본인
- 기수정렬은 낮은 자리수부터 비교하여 정렬해 간다는 것을 기본 개념으로 하는 정렬 알고리즘입니다.
- 기수정렬은 비교 연산을 하지 않으며 정렬 속도가 빠르지만 데이터 전체 크기에 기수 테이블의 크기만한 메모리가 더 필요합니다.
- 0~9 까지의 Bucket(Queue 자료구조의)을 준비합니다.
- 모든 데이터에 대하여 가장 낮은 자리수에 해당하는 Bucket에 차례대로 데이터를 둡니다.
- 0부터 차례대로 버킷에서 데이터를 다시 가져옵니다.
- 가장 높은 자리수를 기준으로 하여 자리수를 높여가며 2번 3번 과정을 반복합니다.
계수 정렬 (Counting Sort)
내용 출처 : https://bowbowbow.tistory.com/8 사진 출처 : 본인
- 첫번째로 각 숫자가 몇번 등장하는지 세어줍니다.
- 등장 횟수를 누적합으로 바꿔줍니다.
- 정렬할 배열 A를 뒤에서 앞으로 순회 하면서 정렬된 배열 B 에 넣어줍니다. 2번 과정에서 구한 누적합이 배열 A의 숫자가 배열 B의 어디에 위치해야 할지 정확하게 알려줍니다.
- A : 정렬 대상
- B : 결과 담을 리스트
- C : A에서 등장한 애들 빈도수 세는 리스트
한계
- 정렬 대상 모두 양의 정수 (일반 정렬에선 정수 아닌 객체 가지고 정렬하는 경우 많아서 제약 많습니다.)
- 숫자 범위 과도하게 크면 메모리가 상당히 낭비됩니다.
Stable sort
- Stable sort란 sorting을 할 경우에 같은 값의 숫자더라도 그 상대적인 위치가 유지되는 sorting 방식입니다.
| Stable sort | Unstable sort |
|---|---|
| Insertion, Merge, Bubble, Counting | Heap, Selection, Quick |
Stable 에 대한 정렬들 세부 비교
Heap, Selection, Quick 은 unstable 입니다.
-
암기 : 셀렉션 아이스크림은 맛나~ 힙퀵
-
1. quicksort
- quicksort 가 stable sorting이 될 수 없는 이유는 예를 들어 1, 1, 1, 5, 2, 3, 4 같은 것을 예시로 알 수 있습니다.
- pivot 원소보다 작거나 같은 것이 있으면 i를 하나 늘리고 A[i]와 A[j]를 바꾸기 때문에 앞의 같은 1이 연속적으로 나오면서 stability가 훼손됩니다.
-
2. heapsort
- 만약 max-heap으로 구현되었다고 치고 40 30 30 20 10을 heapsort로 sorting한다고 해봅니다.
- 그러면 40이 가장 뒤로 가고 앞에 있는 30이 먼저 제거되어 뒤로 보내지게 됩니다.
- 따라서 앞에 있는 30이 뒤에 있는 30보다 더 뒤로 가는 결과를 초래합니다.
- 그러므로 heapsort도 unstable sorting입니다.
-
3. selection sort
- selection sort는 대부분 최대값을 구하는 방법이 가장 첫번째 원소를 최대로 놓고 그것보다 크다면 최대값을 update하는 식이기 때문에 많은 곳에서 stable sort가 아닙니다.
- 하지만 만약 내가 첫번째 원소를 최대로 놓고 그것보다
같거나 크면최대값을 update한다면 selection sort도 stable sort가 될 수 있습니다.
-
4. bubble sort
- 뒤의 값이 앞의 값보다 작다면 두 값을 바꾸는 것이기 때문에 만약 같은 값의 경우에는 순서가 바뀌지 않습니다.
-
5. insertion sort
- 자신보다 큰 값들에 대해서만 index를 하나씩 증가시키고 그 자리에 말 그대로 insert를 하는 sorting이기 때문입니다.
- 만약 이것도 자신보다 크거나 같은 값에 대해 구현한다면 unstable로 만들 수 있습니다. 하지만 거의 대부분의 경우 그렇게 구현하지 않으므로 stable sorting이라고 알고 있으면 됩니다.
-
6. merge sort
- stable sorting 방식입니다. 대신 조건으로, 두 그룹 A, B를 merge 할 경우, 같은 값이 나온다면 앞의 그룹의 숫자를 먼저 가져다 써주어야 합니다. 만약 그렇지 않으면 merge 중에 stability가 훼손될 것입니다.
-
7. counting sort
- counting sort에 대해 알고리즘 구현 방식을 찾아보면 오른쪽에서 왼쪽으로 scan을 하면서 output array에다가 다시 적어주는 형식입니다.
- 마지막 for loop의 순서가 오른쪽에서 왼쪽 (array에서 n-1부터 0까지) 으로 구현되기 때문에 stable sorting이라고 할 수 있습니다.
In-memory sort
- In-memory sort란 추가적인 메모리가 거의 들지 않는 sorting 방식입니다.
| In-memory O | In-memory X |
|---|---|
| Insertion, Selection, Bubble, Heap, Quick | Merge, Counting, Radix, Bucket |
Q) 정렬 시 이진탐색을 사용할 수 있는데, 이진탐색은 중복된 갯수가 몇 개 있는지 추측할 수 없습니다. 이때 이진탐색 bound 개념을 사용해서 이진탐색에서 중복된 갯수를 알 수 있는 방법이 있을까요?
- lower bound
- 타겟보다 같거나 큰 값이 나오는 처음 위치를 반환합니다.
- higher bound : 들어갈 수 있는 범위에서 처음으로
- 타겟보다 처음으로 큰 값이 나오는 위치를 반환합니다.
- 따라서 중복인 갯수를 구하기 위해서는
higher bound - lower bound의 값을 반환하면 됩니다.
-
Random Pivot : Random으로 선택합니다.
-
median - of - three : random index 3개를 뽑은 후, 이 3개가 가리키는 원소들의 median 값으로 pivot을 설정합니다.
- 아닙니다. 이미 정렬된 상황이라면 선택 정렬이 더 유리 (O(N)) 합니다.
- 또한 Quick sort는 최악의 경우 O(N^2) 이기에 항상 최적이라고 할 수 없습니다.
- (1) 최악의 경우 - pivot : pivot이 최소값이나 최댓값으로 선정이 된다면, 나눠진 두 개의 서브 리스트가 불균형하게 되고 이는 퀵 소트의 치명적인 성능 저하로 이어집니다.
- (2) 최악의 경우 - 정렬/역정렬 : 이미 정렬되어 있거나, 역순으로 정렬되어 있는 배열에서는 O(n^2)로 매우 느립니다.
-
- pivot 선택을 최적화
- median three 기법 사용함으로써 최악의 pivot 선택을 방지합니다.
-
- depth를 고려한 인트로 소트 (힙 소트 + 퀵 소트)
- 최악의 경우에도 O(n(log n))의 복잡도를 보장합니다.
- 평소 퀵 소트로 동작하다가 recursion depth가 미리 정해준 레벨보다 깊어지면 힙 소트로 변환하는 하이브리드 방식입니다.
- cache의 효율을 위해 분할된 서브 리스트의 개체수가 16개 이하일 때는 삽입 정렬로 처리하는 것이 훨씬 효과적입니다.
-
-
예 그렇습니다.
-
예 그렇습니다.
- 비재귀는 코드가 방대하고, 종료 조건이 존재하지 않을 시 코드를 어디까지 작성해야할 지 알 수 없기에 재귀를 사용하는 것이 유리한 경우가 있습니다.
-
- 계수 정렬은 인덱스로 구현됩니다. 따라서 양의 정수를 정렬할 시에만 사용가능합니다.
- 숫자 범위가 너무 크면 배열이 지나치게 크게 만들어져 낭비되는 공간이 존재합니다.
- CountingSort는 빠르지만 추가적인 배열을 하나 만들어야 합니다.
- 만약 int타입 배열에 { 1, 10, 1000000 }이 있다면 겨우 3개를 정렬하기 위하여 크기가 최소 1000001인 배열을 만들어야 합니다.
- 정렬해야하는 배열의 크기가 작을 경우 이처럼 비효율적인 상황이 발생하기 때문에 어느정도 크기 이상일 경우에만 사용됩니다.
-
병합 정렬은 추가적인 메모리를 요구하지만 퀵 정렬은 in place 정렬을 수행해 추가적인 메모리를 요구하지 않습니다.
-
퀵 정렬은 pivot을 기준으로 divide 한다면, 병합 정렬은 쪼갤 수 있는 크기까지 divide한다는 차이가 존재합니다.
-
합병 정렬(merge sort)은 리스트를 균등하게 분할하는 것과 달리 퀵 정렬은 리스트를 비균등하게 분할합니다.
Linked List는 삽입, 삭제 시에는 유리하지만 접근 시에 시간 복잡도가 큽니다.
- Linked List를 정렬할 시에 Merge Sort가 유리합니다.
- Merge 정렬은
순차 비교로 정렬을 진행하기에, 접근 및 탐색을 하는 경우가 적어 효율적입니다. - Quick 정렬은 순차 접근이 아닌
임의 접근을 통해 빈번하게 접근과 탐색을 하며 정렬을 진행하기에 비효율적입니다.
- Divide 후 Merge 하는 과정에서
- Linked List는 연결된 포인터의 위치만 변경해주면 돼서 구현이 간단합니다.
- Array는 추가적인 배열 공간을 사용해 병합해야 합니다.
Q) JAVA의 Arrays.sort은 DualPivotQuick Sort, Collections.sort는 Tim Sort알고리즘을 사용합니다. 혹시 100만개의 데이터를 정렬하신다면 어떤 방식으로 정렬하시겠습니까?
- DualPivotQuick는 자칫하면 최악의 경우 (O(N^2)) 시간 복잡도가 발생할 수 있기에, 자료형을 Reference type으로 변경 후 Tim Sort알고리즘(Merge + Selection)을 사용할 수 있도록 유도하는 것이 안정성 측면에서 좋습니다.
Arrays.sort - Dual pivot quick sort
-
배열의 크기가 286이상일 경우
MergeSort를 수행합니다.- 깊이가 O(logN) 보다 깊어지는 경우
-
배열의 크기가 286보다 작은 경우
QuickSort를 MergeSort보다 우선 수행합니다.- 깊이가 O(logN) 보다 깊지 않은 경우 quick 이 더 빠릅니다.
-
배열의 크기가 47보다 작은 경우
InsertionSort를 QuickSort보다 우선 수행합니다.- 길이가 짧은 배열에 대해서는 참조지역성이 높은 삽입정렬이 우세합니다.
- 또한 최선의 경우에는 O(N) 이라는 점에서 짧은 길이에는 삽입정렬 사용합니다.
-
일정 크기 이상의 BYTE, SHORT , CHAR 배열은 COUNTING SORT 가 수행됩니다.
-
CountingSort를 byte, short, char 배열에서만 사용하는 이유는 이 자료형들은 크기가 작아 배열의 값으로 들어갈 범위가 작기 때문입니다.
-
byte배열의 크기가 29보다 큰 경우CountingSort를InsertionSort보다 우선 수행합니다.- CountingSort는 빠르지만 추가적인 배열을 하나 만들어야 합니다.
- 만약 int타입 배열에 { 1, 10, 1000000 }이 있다면 겨우 3개를 정렬하기 위하여 크기가 최소 1000001인 배열을 만들어야 합니다.
- 정렬해야하는 배열의 크기가 작을 경우 이처럼 비효율적인 상황이 발생하기 때문에 어느정도 크기 이상일 경우에만 사용됩니다.
-
short, char 배열의 크기가 3200보다 큰 경우CountingSort를QuickSort보다 우선 수행합니다.
-
-
또한 이 경우 QUICK SORT 는
DualPivotQuicksort방법을 사용합니다.- Pivot을 총 두 개를 선정, 영역을 세 개로 나눔으로써 분할의 이점을 더 높인 알고리즘
- 기존의 SinglePivotQuicksort보다 더 많은 케이스에 대해서 O(nlogn)을 보장합니다.
Collections.sort - Tim Sort
내용 출처 : https://d2.naver.com/helloworld/0315536
참조지역성
- 참조 지역성 원리란, CPU가 미래에 원하는 데이터를 예측하여 속도가 빠른 장치인 캐시 메모리에 담아 놓는데 이때의 예측률을 높이기 위하여 사용하는 원리입니다.
- 최근에 참조한 메모리나 그 메모리와 인접한 메모리를 다시 참조할 확률이 높다는 이론을 기반으로 캐시 메모리에 담아놓는 것입니다.
- 메모리를 연속으로 읽는 작업은 캐시 메모리에서 읽어오기에 빠른 반면, 무작위로 읽는 작업은 메인 메모리에서 읽어오기에 속도의 차이가 있습니다.
| Sort 종류 | 참조 지역성 (C) |
|---|---|
| Heap sort | 한 위치에 있는 요소를 해당 요소의 인덱스 두 배 또는 절반인 요소와 반복적으로 비교하기에 캐시 메모리에서는 예측하기가 매우 어렵습니다. 참조 지역성 (C)는 상대적으로 큽니다 |
| Merge sort | 인접한 덩어리를 병합하기에 참조 지역성의 원리를 어느 정도 잘 만족합니다. 그러나 입력 배열 크기만큼의 메모리를 추가로 사용한다는 단점이 있습니다. |
| Quick sort | pivot 주변에서 데이터의 위치 이동이 빈번하게 발생하기에 참조 지역성이 좋으며 메모리를 추가로 사용하지 않는다. 실제로도 C의 값은 Heap, Merge 정렬들보다 작은 값으로 정의되어 있고 평균 시간 복잡도는 셋 중에 가장 빠르다고 알려져 있습니다. |
| Insertion sort | 인접한 메모리와의 비교를 반복하기에 참조 지역성의 원리를 잘 만족합니다. |
- Insertion sort는 인접한 메모리와의 비교를 반복하기에 참조 지역성의 원리를 매우 잘 만족합니다.
- 이때 Quick sort 또한 참조 지역성의 원리를 매우 잘 만족합니다.
- 이 둘을 비교해보면 아래와 같습니다. (삽입의 C 를 Ci로 두고 퀵의 C를 Cq로 두었을 때 )

- 이에 따라 작은 n에 대하여 Insertion sort가 빠릅니다.
- 이것을 이용하여 전체를 작은 덩어리로 잘라 각각의 덩어리를 Insertion sort로 정렬한 뒤 병합하면 좀 더 빠르지 않을까 하는 것이 기본적인 아이디어에서 비롯됐다고 합니다.

Tim Sort의 추가적인 성능 최적화 기법
-
- Binary Insertion sort
- Tim sort에서 사용하는 Insertion sort는 Binary Insertion sort를 사용합니다.
- Binary라는 용어에서 알 수 있듯이, 삽입해야 할 위치를 찾을 때까지 비교하는 대신, 앞의 원소들은 모두 정렬되어 있다는 전제를 기반으로 이분 탐색을 진행하여 위치를 찾습니다.
- 이분 탐색은 참조 지역성은 떨어지지만 한 원소를 삽입할 때 O(N) 번의 비교가 아닌 O(logN) 만큼의 비교만 수행합니다.
- 삽입해야 할 위치를 빠르게 찾아도 그 위치에 삽입하는 과정은 O(N)이기에 전체의 시간 복잡도는 O(N^2)으로 일반적인 Insertion sort와 동일하지만, 그 위치에 삽입하고 나머지 원소를 시프트하는 연산은 빠르기 때문에 훨씬 효율적입니다.
-
- 비슷한 크기의 덩어리끼리 Merge
- Tim sort에서는 하나의 run이 만들어질 때마다 스택에 담아 효율적으로 병합을 진행합니다.
- 이때 run을 스택에 push할 때마다 스택의 맨 위의 세 run이 그림과 같이 두 조건을 만족해야 하며 비슷한 길이의 덩어리끼리 merge를 진행합니다.

-
- 추가 메모리 사용 최소화
- 병합을 진행할 때 최악의 경우 O(N/2)의 추가 메모리를 사용합니다. 비록 Merge sort와 같은 O(N)의 추가 메모리를 사용하지만 절반을 절약할 수 있습니다.
-
index를 이용해서 왼쪽, 오른쪽 자식 노드를 표기합니다.
-
왼쪽 노드 : 자기자신 idx * 2
-
오른쪽 노드 : 자기자신 idx * 2 + 1
- 이진 트리는 최대 높이가 O(logN) 입니다.
- N개의 원소를 정렬할 때 N개의 원소를 트리 루트로 올려주는 과정이 필요하기에 heapfiy를 N번 수행해주어야 합니다.
- 이때 heapfiy는 트리 높이 만큼인 O(logN)이 걸리는 데, 이를 N번 수행해주기에 N번*O(logN) <N번의 heapfiy>, 즉 O(NlogN)의 시간복잡도가 소요됩니다.
-
- Merge보다 Quick 이 빠릅니다.
-
재정렬 + 메모리 재사용 여부
- Merge 는 병합 과정의 왼쪽, 오른쪽 데이터를 merge 시에 또 다시 정렬을 진행해야 합니다. 또한 이 과정에서 임시 배열을 하나 더 사용합니다. (재정렬 + 메모리 재사용)
- 반면에 Quick 은 원 배열을 부분 배열로 분할하지만, 병합과정은 거치지 않습니다. 즉 , 임시 배열을 만들거나 재정렬하지 않아 더 빠릅니다.
-
참조지역성 관점
Sort 종류 참조 지역성 (C) Merge sort 인접한 덩어리를 병합하기에 참조 지역성의 원리를 어느 정도 잘 만족합니다. 그러나 입력 배열 크기만큼의 메모리를 추가로 사용한다는 단점이 있습니다. Quick sort pivot 주변에서 데이터의 위치 이동이 빈번하게 발생하기에 참조 지역성이 좋으며 메모리를 추가로 사용하지 않는다. 실제로도 C의 값은 Heap, Merge 정렬들보다 작은 값으로 정의되어 있고 평균 시간 복잡도는 셋 중에 가장 빠르다고 알려져 있습니다. -
Merge보다 Quick이 참조지역성이 더 좋습니다.
-
따라서 Quick으로 기존 캐시에 있던 데이터를 활용하기가 좋아 cache hit가 빈번하게 발생하며 더 빠릅니다.
-
-
- Merge는 stable, Quick은 Unstable 합니다.
-
- Merge는 최악이 O(NlogN), Quick은 O(N^2) 입니다.
-
- Linked List 정렬 시
- Merge 정렬은
순차 비교로 정렬을 진행하기에, 접근 및 탐색을 하는 경우가 적어 효율적입니다. - Quick 정렬은 순차 접근이 아닌
임의 접근을 통해 빈번하게 접근과 탐색을 하며 정렬을 진행하기에 비효율적입니다.
- Merge 정렬은
- Linked List 정렬 시
https://ko.wikipedia.org/wiki/%EC%A0%95%EB%A0%AC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://underdog11.tistory.com
https://d2.naver.com/helloworld/0315536
https://lemonlemon.tistory.com/136








