Skip to content

Latest commit

 

History

History
775 lines (521 loc) · 23.7 KB

Information_Retrieval.md

File metadata and controls

775 lines (521 loc) · 23.7 KB

Information Retrieval - Topic Modelling Relevent Part

Overview

Information Retrieval Model

Wiki IR Model

MIR IR Model Summary

Four characters in Information Retrieval Model

  • $D$: Documents
  • $Q$: Query
  • $F$: Framework (i.e. chosen Model)
  • $R(q_i, d_j)$: Ordering (Ranking) funciton

$$ \text{Information Retreival Model} = [D, Q, F, R(q_i, d_j)] $$

MIR IR Model

Relevant Searching

$$ \text{Relevant} = f(Q, d_j, D) $$

Classical Information Retrieval Model

(usually work with unstructured text document)

Set-theoretic Models:

Set-theoretic models represent documents as sets of words or phrases. Similarities are usually derived from set-theoretic operations on those sets.

Algebraic Models:

Algebraic models represent documents and queries usually as vectors, matrices, or tuples. The similarity of the query vector and document vector is represented as a scalar value.

Probabilistic Models:

Probabilistic models treat the process of document retrieval as a probabilistic inference. Similarities are computed as probabilities that a document is relevant for a given query. Probabilistic theorems like the Bayes' theorem are often used in these models.

  • Binary Independence Model
  • Probabilistic Relevance Model (on which is based the okapi (BM25) relevance function)
  • Uncertain Inference
  • Language Models
  • Divergence-from-randomness Model
  • Latent Dirichlet Allocation

Semi-structured Document Information Retrieval Model

  • XML

Link-based Information Retrieval Model

Multimedia Information Retrieval Model

  • Image
  • Audio and Music
  • Video

How to represent text

Term Weight

Inverted Index

Performance and Correctness Measures

The Document Collections

  • Pooling Method

Standard Relevance Benchmarks

  • The TREC Web Collections
  • INEX
  • Reuters, OHSUMED, NewsGroups
  • NTCIR
  • CLEF
  • GOV2

Text Representation

Bag-of-words Approach

Wiki - Bag-of-words model

  • Treat all the words in a document as index terms for that document
  • Assign a weight to each term based on its importance
  • Disregard order, structure, meaning, etc. of the words

Conclusion

  • This approach think IR is all (and only) about mathcing words in documents with words in queries (which is not true)
  • But it works pretty well

Vector Representation

  • "Bags of words" can be represented as vectors
    • For computational efficiency, easy of manipulation
    • Geometric metaphor: "arrows"
  • A vector is a set of values recorded in any consistent order

Term Weighting

Term:

The definition of term depends on the application. (Typically terms are single words, keywords, or longer phrases.)

  • Each dimension corresponds to a separate term.
  • If a term occurs in the document, its value in the vector is non-zero.
  • If words are chosen to be the terms, the dimensionality of the vector is the number of words in the vocabulary (the number of distinct words occurring in the corpus).

Example:

document text terms
doc1 ant ant bee ant bee
doc2 dog bee dog hog dog ant dog ant bee dog hog
doc3 cat gnu dog eel fox cat dog eel fox gnu
query content
q ant dog

Term incidence matrix (in Term vector space (No weighting)):

doc ant bee cat dog eel fox gnu hog
doc1 1 1
doc2 1 1 1 1
doc3 1 1 1 1 1

(boolean model)

Unnormalized Form of Term Frequency (TF) (weighting):

(Weight of term td) = frequency that term j occurs in document i

doc ant bee cat dog eel fox gnu hog length
doc1 2 1 $\sqrt{5}$
doc2 1 1 4 1 $\sqrt{19}$
doc3 1 1 1 1 1 $\sqrt{5}$

Calculate Ranking:

(cosine) Similarity of documents (vector space model)

  • |doc1|doc2|doc3 ----|:--:|:--:|:--: doc1| 1 |0.31| 0 doc2|0.31| 1 |0.41 doc3| 0 |0.41| 1

Similarity of query to documents

  • |doc1|doc2|doc3 ----|:--:|:--:|:--: q |0.63|0.81|0.32

Methods for Selecting Weights:

  • Empirical

    Test a large number of possible weighting schemes with actual data

  • Model based

    Develoop a mathematical model of word distribution and derive weighting scheme theoretically. (e.g Probabilistic model)

  • Intuition

    • Terms that appear often in a document should get higher weights
      • The more often a document contains the term "dog", the more likely that the document is "about" dogs
    • Terms that appear in many documents should get low weights
      • Words like "the", "a", "of" appear in (nearly) all documents

  • Weighting scheme

    • bianry (i.e. term incidence matrix)
    • row count (i.e. unnormalized form of term frequency)
    • term frequency (the following thing...)
    • log normalization
    • double normalization 0.5
    • double normalization K
    • ...

TF-IDF

  • TF stands for Term Frequency
  • IDF stands for Inverse Document Frequency

Term Frequency

($t$ stands for term; $d$ stands for document)

$$ tf(t, d) = f_{t, d} $$

Concept:

  • A term that appears many times within a document is likely to be more important than a term that appears only once

Normalization (for Free-text document):

Key: Length of document

  • a term frequency in different length of document may have different importance

Maximum Normalization:

$$ tf(t, d) = \frac{f_{t, d}}{\text{maximum frequency of any term in document}d}= \frac{f{t, d}}{\max_{t' \in d}(f_{t, d})} = \frac{f_{t, d}}{m_d} $$

Augmented Maximum Normalization: (for Structured Text)

(Salton and Buckley recommend K = 0.5)

$$ tf(t, d) = K + (1-K) \times \frac{f_{t, d}}{m_d}, K \in [0, 1] $$

Cosine Normalization:

$$ tf(t, d) = \frac{f_{t, d}}{\sqrt{\sum_{d}(f_{t, d})^2}} $$

Inverse Document Frequency

Concept:

  • A term that occurs in only a few documents is likely to be a better discriminator that a term that appears in most or all documents

A Simple Method: use document frequency

$$ idf(t, D) = \frac{1}{df} = \frac{1}{\frac{\text{number of document has term}_j}{\text{number of total documents}}} = \frac{|D|}{n_t} $$

(the simple method over-emphasizes small differences) => use logarithm

A Standard Method: use log form

$$ idf(t, D) = \log(\frac{N}{n_t}) + 1 $$

Full weighting of TF-IDF

The weight assigned to term $t$ in document $d$:

$$ \mathit{tf.idf}(t, d, D) = tf(t, d) \times idf(t, D) $$

Example:

$$ \mathit{tf.idf}(t, d, D) = \underbrace{\frac{f_{t, d}}{m_t}}{tf(t, d)} \times \underbrace{(\log(\frac{N}{n_t}) + 1)}{idf(t, D)} $$

Inverted Index

TBD

IR Models

Boolean Model

Brief description:

  • Based on notion of sets
  • Documents are retrieved only if they satisfy boolean conditions specified in the query
  • No ranking on retrieved documents (can't have order)
  • Exact match (don't support fuzzy match)

Similarity of documnet and query:

$$ \mathit{Sim}(\mathbf{doc}_i, \mathbf{query}) \begin{cases} 1, \exists c(\mathbf{query})|c(\mathbf{query}) = c(\mathbf{doc}_i) \\ 0, \text{otherwise} \end{cases} $$

Boolean Retreival

(Boolean operators approximate natural language)

  • AND: discover relationships between concepts
  • OR: discover alternate terminology
  • NOT: discover alternate meaning

The Perfect Query Paradox

  • Every information need has a perfect set of documents
    • If not, there would be no sense doing retrieval
  • Every document set has a perfect query
    • AND every word in a document to get a query for it
    • Repeat for each document in the set
    • OR every document query to get the set query

but can users realistically be expected to formulate this perfect query? => perfact query formulation is hard

Why Boolean Retrieval Fails

  • Natural language is way more complex
  • AND "discovers" nonexistent relationships
    • Terms in different sentences, paragraphs, ...
  • Guessing terminology for OR is hard
    • e.g. good, nice, excellent, outstanding, awesome, ...
  • Guessing terms to exclude is even harder
    • e.g. democratic party, party to a lawsuit, ...

Pros and Cons

  • Strengths
    • Precise
      • if you know the right strategies
      • if you have an idea of what you're looking for
    • Efficient for the computer
  • Weaknesses
    • User must learn boolean logic
    • Boolean logic insufficient to capture the richness of language
    • No control over size of result set (either too many documents or none)
    • When do you stop reading? All documents in the result set are considered "equally good"
    • What about partial matches? Documents that "don't quite match" the query may be useful also

Ranked Retrieval

Arranging documents by relevance

  • Closer to how humans think
    • some documents are "better" than others
  • Closer to user behavior
    • users can decide when to stop reading
  • Best (partial) match
    • documents need not have all query terms

Similarity-Based Queries

  • Replace relevance with similarity
    • rank documents by their similarity with the query
  • Treat the query as if it were a document
    • Create a query bag-of-words
    • Find its similarity to each document
    • Rank by sorting the document with similarity

Vector Space Model

Brief description:

  • Based on geometry, the notion of vectors in high dimensional space
  • Documents are ranked based on their similarity to the query (ranked retrieval)
  • Best / partial match

Postulate: Documents that are "close together" in vector space "talk about" the same things

Therefore, retrieve documents based on how close the document is to the query (i.e. similarity ~ "closeness")

Similarity of document and query:

$$ \mathit{Sim}(\mathbf{doc}_i, \mathbf{query}) = \cos{\theta} = \frac{\mathbf{doc}_i \cdot \mathbf{query}}{\left| \mathbf{doc}_i \right| \left | \mathbf{query} \right|} $$

Fuzzy Set Model

Fuzzy Set:

Operations

  • NOT ${\displaystyle \forall x\in {U}:\mu _{\neg {A}}(x)=1-\mu _{A}(x)}$
  • AND ${\displaystyle \forall x\in {U}:\mu _{A\cap {B}}(x)=t(\mu _{A}(x),\mu _{B}(x))}$
  • OR ${\displaystyle \forall x\in {U}:\mu _{A\cup {B}}(x)=s(\mu _{A}(x),\mu _{B}(x))}$

Extended Boolean Model

The weight of term Kx associated with document dj is measured by its normalized Term frequency

${\displaystyle w_{x,j}=f_{x,j}*{\frac {Idf_{x}}{max_{i}Idf_{i}}}}$

  • P-norms ($L^\textit{p}\text{-norm}$): extends the notion of distance to include p-distances, where 1 ≤ p ≤ ∞ is a new parameter
    • p = 1, similarity like vector space model
    • p = ∞, similarity like fuzzy set model

Euclidean distances similarity

${\displaystyle q_{or}=k_{1}\lor ^{p}k_{2}\lor ^{p}....\lor ^{p}k_{t}}$

$$ {\displaystyle sim(q_{or},d_{j})={\sqrt[{p}]{\frac {w_{1}^{p}+w_{2}^{p}+....+w_{t}^{p}}{t}}}} $$

${\displaystyle q_{and}=k_{1}\land ^{p}k_{2}\land ^{p}....\land ^{p}k_{t}}$

$$ {\displaystyle sim(q_{and},d_{j})=1-{\sqrt[{p}]{\frac {(1-w_{1})^{p}+(1-w_{2})^{p}+....+(1-w_{t})^{p}}{t}}}} $$

Summary

  • Include boolean, vector space, fuzzy set in one model (framework)

Generalized Vector Space Model

Similarity

$$ {\displaystyle sim(d_{k},q)={\frac {\sum {j=1}^{n}\sum {i=1}^{n}w{i,k}\times wgma{j,q}\times t_{i}\cdot t_{j}}{{\sqrt {\sum {i=1}^{n}w{i,k}^{2}}}\times {\sqrt {\sum {i=1}^{n}w{i,q}^{2}}}}}} $$

Latent Semantic Analysis (Latent Semantic Indexing)

Dimensionality reduction using truncated SVD (aka LSA)

In particular, truncated SVD works on term count/tf-idf matrices. In that context, it is known as latent semantic analysis (LSA).

This estimator supports two algorithms: a fast randomized SVD solver, and a “naive” algorithm that uses ARPACK as an eigensolver on (X * X.T) or (X.T * X), whichever is more efficient.

Doc-Term Matrix (like User-Item Rating Matrix in Recommendation System)

Ranked similarity by TF-IDF

Evaluation Measures

Wiki - Evaluation measures (information retrieval)

What IR evaluate for?

  • Efficiency
    • retrieval time
    • indexing time
    • index size
  • Effectiveness
    • how "good" are the documents that are returned?
    • system only / human + system
  • Usability
    • learnability
    • frustration
    • novice vs. expert users
  • Others
    • coverage
    • update frequency
    • visit rate
    • ...

Test collection: a laboratory environment that doesn’t change

  • determine how well IR systems perform
  • compare the performance of the IR system with that of other systems
  • compare search alghoritms and strategies with each other

The Cranfield Paradigm: provided a foundation for the evaluation of IR systems => Precision ration and Recall ratio

Set-Based Measures

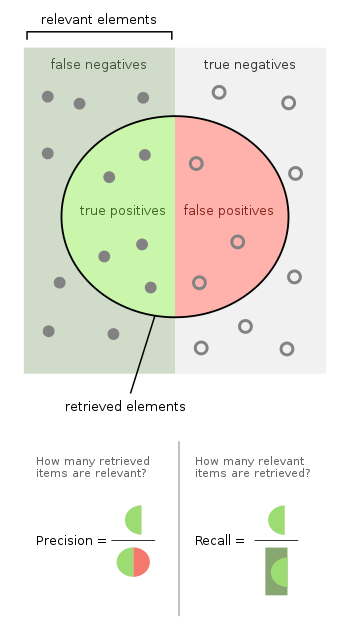
Wiki Precision and Recall

R and A venn diagram

Answer \ Relevant element Relevant Not relevant
Retrieved True Positive (TP) False Positive (FP)
Not Retrieved False Negative (FN) True Negative (TN)
  • $R$ (Relevant documents) = $TP + FP$
  • $A$ (Answer, Retrieved docuemtnt) = $TP + FN$ (documents which we thought to be the answer)
  • Collection size = $TP + FP$ + $FP$ + $TN$ = $R\cup A$

Precision

$\displaystyle\text{Precision} = \frac{TP}{(TP + FP)} = \frac{|R\cap A|}{|A|} = \frac{|{\text{relevant documents}}\cap{\text{retrieved documents}}|}{|{\text{retrieved documents}}|}$

  • the fraction of documents retrieved that are relevant

Recall

$\displaystyle\text{Recall} = \frac{TP}{(TP + FN)} = \frac{|R\cap A|}{|R|} = \frac{|{\text{relevant documents}}\cap{\text{retrieved documents}}|}{|{\text{relevant documents}}|}$

  • the fraction of relevant documents retrieved
  • hard to compute (need to know all the relevant document) => Pooling Method

Miss = $\displaystyle\frac{FN}{(TP + FN)}$

  • the inverse of precision

False alarm (fallout) = $\displaystyle\frac{FP}{(FP + TN)}$

Single Value Summaries

P@n

Precision at n

  • P@5, n = 5
  • P@10, n = 10
  • P@20, n = 20
  • Consider user usually only care the first page (or the top n) search result

R-Precision

MAP (Mean Average Precision)

Precision-Recall Curve

TBD

AP

  • The idea here is to average the precision figures obtained after each new relevant document is observed
    • For each query, we calculate precision for each recall
    • Each time we found a new relevent document => get a new recall
      • Precision = # of Relevent / Current found documents
    • For relevant documents not retrieved, the precision is set to 0
    • Invoke average at the end
  • Interpolation
    • Fill the recall to 10% 20% ... 100% base

MAP

Mean of every query's AP

$$ \operatorname{MAP} = \frac{\sum_{q=1}^Q \operatorname{AveP(q)}}{Q} ! $$

  • System comparison

MRR (Mean Reciproach Rank)

$$ {\text{MRR}}={\frac {1}{|Q|}}\sum {{i=1}}^{{|Q|}}{\frac {1}{{\text{rank}}{i}}} $$

F Measure: Harmonic means of Precision and Recall

Wiki - F1 score

The traditional F-measure or balanced F-score (F1 score) is the harmonic mean of precision and recall

$$ {\displaystyle F_{1}=\left({\frac {\mathrm {recall} ^{-1}+\mathrm {precision} ^{-1}}{2}}\right)^{-1}=2\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{\mathrm {precision} +\mathrm {recall} }}} = \frac{2}{\frac{1}{P} + \frac{1}{R}} $$

The general formula for positive real β

$$ F_\beta = (1 + \beta^2) \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{(\beta^2 \cdot \mathrm{precision}) + \mathrm{recall}} $$

E Measure

$$ {\displaystyle E=1-\left({\frac {\alpha }{p}}+{\frac {1-\alpha }{r}}\right)^{-1}} $$

Their relationship is $F_{\beta }=1-E$ where ${\displaystyle \alpha ={\frac {1}{1+\beta ^{2}}}}$

User-Oriented Measures

User-Oriented Measures

Coverage Ratio

$$ \operatorname{coverage} = \frac{|K \cap R \cap A|}{|K \cap R|} $$

Novely Ratio

$$ \operatorname{novelty} = \frac{|(R \cap A) - K|}{|K \cap R|} $$

Relative Recall

Recall Effort

Discounted Cumulative Gain (DCG)

Wiki - Discounted cumulative gain

CG (Cumulative Gain)

$$ {\mathrm {CG_{{p}}}}=\sum {{i=1}}^{{p}}rel{{i}} = rel_1 + rel_2 + \dots + rel_p $$

DCG

$$ {\displaystyle \mathrm {DCG_{p}} =\sum {i=1}^{p}{\frac {rel{i}}{\log {2}(i+1)}}=rel{1}+\sum {i=2}^{p}{\frac {rel{i}}{\log _{2}(i+1)}}} = rel_1 + \frac{rel_2}{\log_2 3} + \dots + \frac{rel_p}{\log_2 p+1} $$

NDCG (Normalized DCG)

$$ {\mathrm {nDCG_{{p}}}}={\frac {DCG_{{p}}}{IDCG_{{p}}}}, $$

where IDCG is ideal discounted cumulative gain, ${\displaystyle \mathrm {IDCG_{p}} =\sum {i=1}^{|REL|}{\frac {2^{rel{i}}-1}{\log _{2}(i+1)}}}$ and ${\displaystyle |REL|}$ represents the list of relevant documents (ordered by their relevance) in the corpus up to position p.

Document Collections

Pooling Method

The technique of assessing relevance

The set of relevant documents for each topic is obtained from a pool of possible relevant documents

  • This pool is created by taking the top K documents (usually, K = 100) in the rankings generated by various retrieval systems
  • The documents in the pool are then shown to human assessors who ultimately decide on the relevance of each document

The TREC Web Collection

Link Analysis

Page Rank

Wiki - PageRank

HITS (Hypertext Induced Topic Search)

Wiki - HITS algorithm

  • Authority
    • Authorities stemmed from a particular insight into the creation of web pages when the Internet was originally forming
  • Hub
    • A certain web pages, known as hubs, served as large directories that were not actually authoritative in the information that they held, but were used as compilations of a broad catalog of information that led users direct to other authoritative pages
  • Summary
    • In other words, a good hub represented a page that pointed to many other pages, and a good authority represented a page that was linked by many different hubs.

Authority update rule

$$ {\mathrm {auth}}(p)=\displaystyle \sum _{{i=1}}^{n}{\mathrm {hub}}(i) $$

Hub update rule

$$ {\mathrm {hub}}(p)=\displaystyle \sum _{{i=1}}^{n}{\mathrm {auth}}(i) $$

Reference

Book

  • Modern Information Retrieval - The Concepts and Technology behind Search
    • Ch 3 Modelling
      • Ch 3.2.2 Boolean Model
      • Ch 3.2.6 Vector Space Model
        • Ch 3.2.5 Document Length Normalization
      • Ch 3.3.2 Expended Boolean Model
      • Ch 3.3.3 Model based on Fuzzy Set
      • Ch 3.4.1 Generalized Vector Space Model
      • Ch 3.4.2 LSI Model
    • Ch 3.2.3 Term weight
      • Ch 3.2.4 TF-IDF
    • Ch 4 Evaluation
      • Ch 4.2 The Cranfield Paradigm
      • Ch 4.3 Measures
        • Ch 4.3.1 Precision / Recall
        • Ch 4.3.2 Single Value Summaries
        • Ch 4.3.3 User-Oriented Measures
        • Ch 4.3.4 Discounted Cumulative Gain
      • Ch 4.4 The Document Collections
        • Ch 4.4.1 The TREC Web Collection
    • Ch 11.5.2 Sorting based on link

Download all the slides

curl -O http://www.just.edu.jo/\~hmeidi/Teaching/CS721/slides_chap\[01-17\].pdf

PengBo's slides (Web Based Information Architecture)

  • Introduction to Information Retrieval
    • Ch 1.2 A first take at building an inverted index
    • Ch 1.4 The extended Boolean model versus ranked retrieval
    • Ch 6.2 Term frequency and weighting
      • Ch 6.2.1 Inverse document frequency
      • Ch 6.2.2 Tf-idf weighting
      • Ch 6.4 Variant tf-idf functions