forked from albertotb/curso-ml-R
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy path12-nn.html
925 lines (569 loc) · 23.8 KB
/
12-nn.html
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml" lang="" xml:lang="">
<head>
<title>Redes neuronales</title>
<meta charset="utf-8" />
<meta name="author" content="Alberto Torres Barrán y Roi Naveiro" />
<meta name="date" content="2019-06-04" />
<link href="libs/remark-css-0.0.1/default.css" rel="stylesheet" />
<link rel="stylesheet" href="custom.css" type="text/css" />
</head>
<body>
<textarea id="source">
class: center, middle, inverse, title-slide
# Redes neuronales
## Curso de aprendizaje automático para el INE
### Alberto Torres Barrán y Roi Naveiro
### 2019-06-04
---
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
TeX: {
Macros: {
Xcal: "{\\mathcal{X}}",
Xbf: "{\\mathbf{X}}",
Qbf: "{\\mathbf{Q}}",
Zbf: "{\\mathbf{Z}}",
Vbf: "{\\mathbf{V}}",
Hbf: "{\\mathbf{H}}",
Rbb: "{\\mathbb{R}}"
},
extensions: ["AMSmath.js","AMSsymbols.js"]
}
});
</script>
---
class: middle, center, inverse
# Introducción
---
## Perceptrón
* Combinación lineal de las variables de entrada
* No linealidad: función de activación (por ejemplo la función escalón)
.center[

[Fuente](https://towardsdatascience.com/perceptron-the-artificial-neuron-4d8c70d5cc8d)
]
---
## Ejemplo perceptron
[
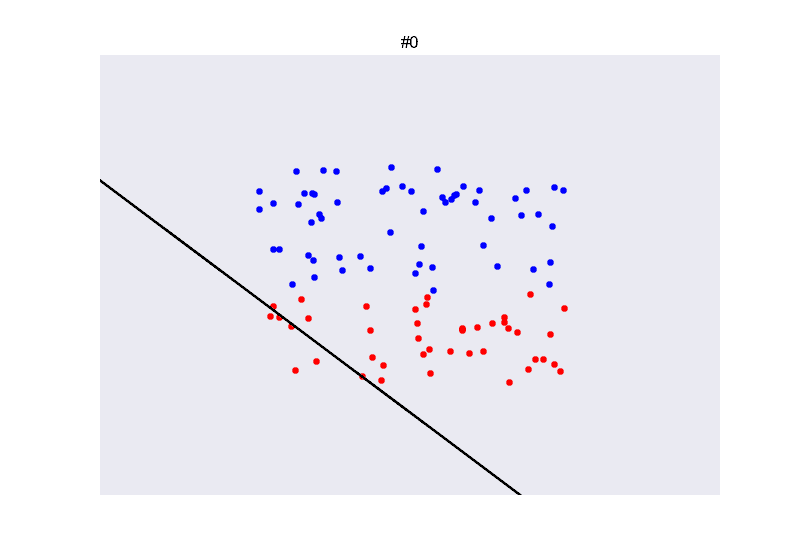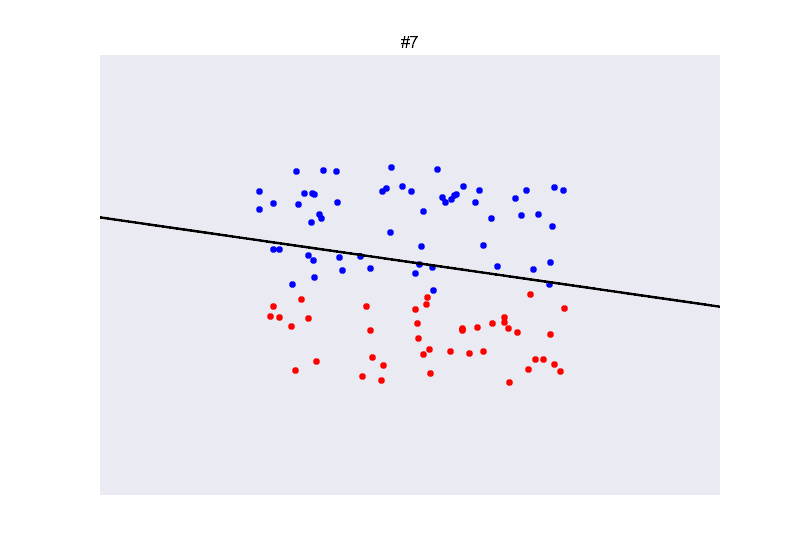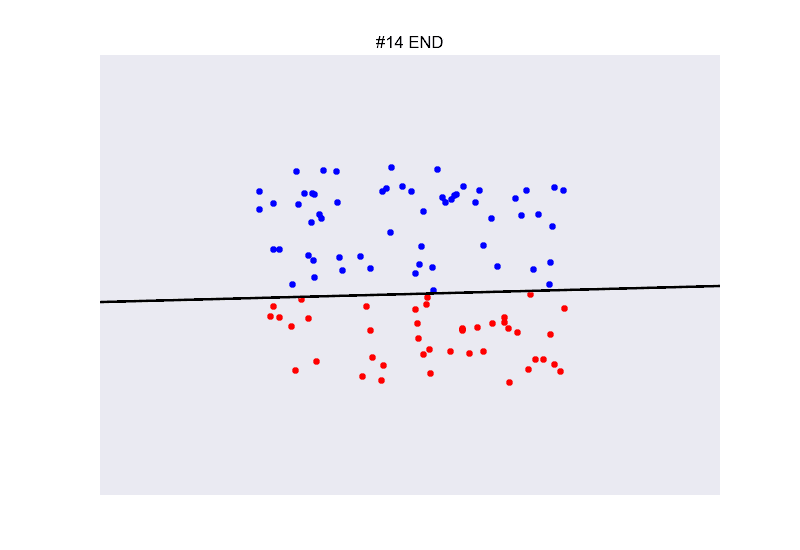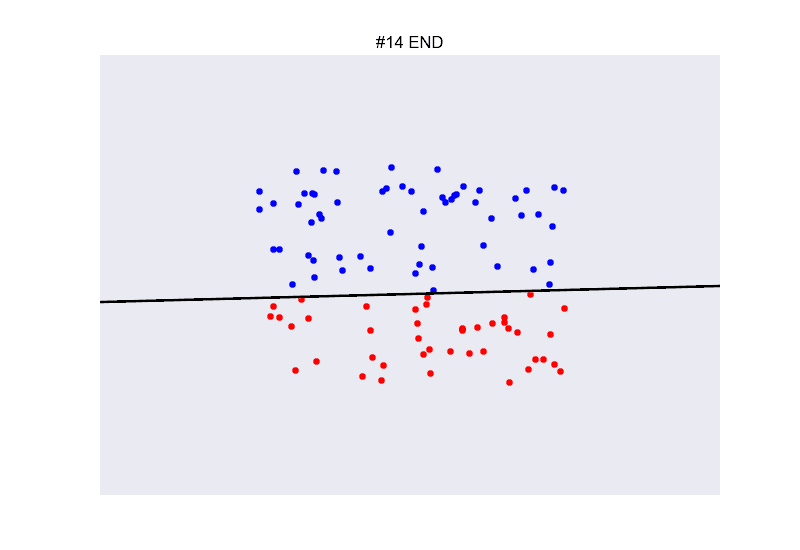](https://github.com/miku/nntour)
---
## Problema XOR
* Observaciones no separables linealmente `\(\Rightarrow\)` perceptrón no encuentra solución
.center[
[Fuente](https://www.freecodecamp.org/news/the-history-of-deep-learning-explored-through-6-code-snippets-d0a0e8545202/)
]
---
## Redes neuronales
* Añadimos una capa intermedia (capa oculta)
.center[

[Fuente](https://en.wikipedia.org/wiki/Artificial_neural_network)
]
---
## Teorema de aproximación universal
* Asumimos:
- red neuronal feed-forward
- una capa oculta
- número de neuronas finito
- algunas funciones de activación (por ej. sigmoidea)
* Aproxima cualquier función continua con precisión arbitrarea
* **Pero**:el número de neuronas necesario es exponencialmente grande
---
## Aprender representaciones
* Modelos como las SVMs generan una nueva representación de los datos de entrada en un espacio ampliado
* Esperamos que en este nuevo espacio el problema de aprendizaje sea más sencillo
* Esta nueva representación también se puede generar de forma manual (*feature engineering*)
* Crear nuevas variables es, típicamente:
1. critico para obtener buen rendimiento
2. muy dependiente del problema
* Ejemplo: extraer variables de datos no tabulares (audio, video, imágenes, texto)
---
class: center, middle

---
## RN vs otros modelos
* Automatizan la creación de nuevas variables
* Esto simplifica la resolución de nuevos problemas:
1. no necesario tanto conocimiento específico
2. proceso mucho menos costoso que crear nuevas variables a mano
* Además la creación de estas nuevas representaciones forma parte del aprendizaje
* específicas para la tarea a resolver `\(\Rightarrow\)` mejor rendimiento
---
class: center, middle

---
## Ejemplo
* Clasificar imágenes médicas en sano/enfermo
* Antes: una parte importante del trabajo consistía en procesar las imágenes del microscopio para extraer características:
1. segmentar células
2. identificar núcleo
3. etc.
* Redes neuronales profundas extraen automáticamente características **útiles para la tarea de clasificar**
.center[

]
---
## ¿Por qué ahora?
* Redes convolucionales y *backpropagation* son de 1989
* Redes recurrentes como la LSTM de 1997
* Desde 2010 varios avances han contribuido al exíto de las redes neuronales:
1. hardware
2. datos
3. avances algorítmicos
---
## Hardware
* Entre 1990 y 2010 las CPUs estándar incrementaron su velocidad un factor de 5000
* Modelos de redes neuronales entrenables en un portátil estándar
* No suficiente para modelos más complejos (recurrentes, convolucionales)
* GPUs: unidades de procesamiento gráfico
1. procesadores más sencillos
2. útiles para procesar grandes bloques de datos en paralelo
* Entrenar una red necesita muchas multiplicaciones de matrices
* NVIDIA Titan X (aprox. 1000$) tiene 350 veces más potencia que un portátil moderno `\(\Rightarrow\)` 6.6 trillones de operaciones en coma flotante/segundo
---
## Datos
* Desarrollo exponencial de la capacidad de almacenamiento
* Internet: recolectar y distribuir conjuntos de datos de forma sencilla
1. Wikipedia (texto)
2. Youtube (video)
3. Flickr (imágenes)
* Competiciones de benchmark, por ej. ImageNet o Kaggle
---
## Algoritmos
* Hasta 2010 no existían formas fiables de entrenar redes neuronales profundas (solo 1 o 2 capas)
1. se puede calcular el gradiente (*backpropagation*)
2. la señal del error se desvanece en las capas intermedias
* Ciertos avances algorítmicos aliviaron el problema:
1. mejores funciones de activación
2. mejor inicialización de los pesos
3. mejores algoritmos de optimización (variantes de SGD)
* Se pueden entrenar redes con 10 o más capas
* Hoy en día otros avances permiten entrenar modelos con cientos de capas
---
## Ventajas y desventajas
Ventajas
* Simplicidad: no es necesario crear nuevas variables a mano
* Escalabilidad:
1. paralelizacion en GPUs
2. uso de mini-baches
* Versatilidad y reusabilidad:
1. aprovechar representaciones aprendidas para otros problemas
2. continuar el entrenamiento con nuevos datos
Desventajas
* Coste computacional y hardware
* Dificultad entrenamiento
---
## Democratización
* Antes: programar en GPUs `\(\Rightarrow\)` lenguajes específicos (CUDA) y C++
* Desde 2010: multiples librerias (Torch, Theano, Caffe, Tensorflow) que
1. realizan diferenciación automática
2. implementan tensores y operaciones con los mismos
3. hacen uso de la GPU de forma transparente
* Ahora: varias librerías de alto nivel que implementan capas de aprendizaje profundo:
1. **Keras**
2. PyTorch
---
## Ejemplo Keras
* Problema de regresión con 2 salidas
* Arquitectura:
.center[

]
---
```r
library(keras)
model <- keras_model_sequential()
# arquitectura
model %>%
layer_dense(units = 4,
activation = 'sigmoid',
input_shape = c(3)) %>%
layer_dense(units = 2,
activation = 'linear')
# definir entrenamiento
model %>% compile(loss = "mse",
optimizer = optimizer_sgd())
# entrenamiento
model %>% fit(X_train, y_train,
epochs = 10, batch_size = 128,
validation_size = 0.2)
# error de test
model %>% evaluate(X_test)
```
---
class: middle, center, inverse
# Perceptrón multicapa
---
## Introducción
* Hasta ahora hemos visto modelos de regresión y clasificación que recibían como input combinaciones lineales de *funciones base*.
* Para que estos modelos resulten prácticos, debemos adaptar las funciones base a los datos.
* Idea:
1. Fijar el número de funciones base de antemano
2. Darles forma paramétrica
3. Aprender parámetros usando los datos.
* **Aprender la representación**.
* *Perceptrón multicapa* o *feed-forward neural network*.
---
## Perceptrón multicapa (1)
* ¿Cómo parametrizamos las funciones de base?
* Hasta ahora
`\begin{equation}
y(x,w) = f \left( \sum_{j=1}^M w_j \phi_j(x) \right)
\end{equation}`
* Siendo `\(f\)` una **activación no lineal**.
* Objetivo: parametrizar `\(\phi_j(x)\)` y aprender los parámetros.
* Idea de las NN: parametrizar `\(\phi_j(x)\)` de la misma manera que `\(y(x,w)\)`.
---
## Perceptrón multicapa (2)
* MLP básico:
1. Construír `\(M\)` combinaciones lineales del input `\(x_1, \dots, x_D\)`:
`\begin{equation}
a_j = \sum_{i=1}^D w_{ji}^{(1)} x_i + w_{j0}
\end{equation}`
2. Transformar cada activación `\(a_j\)` usando una función de activación **no lineal** y **diferenciable**: `\(z_j = h(a_j)\)`.
3. Repetir 1 y 2, tantas veces como **capas ocultas** queramos en la red.
4. Por último, en la capa de salida, las activaciones se transforman con una función de activación adecuada para producir los outputs `\(y_k\)`.
* Notación: `\(w_{ji}\)` son *pesos*, `\(w_{j0}\)` son *biases*, `\(a_j\)` son *activaciones*.
---
## Perceptrón multicapa (3)
* **Ejercicio**: ¿Por qué las activaciones tienen que ser funciones no lineales diferenciables?
---
## Perceptrón multicapa (4)
* La función de activación de la capa de salida, dependerá de la naturaleza de los datos.
* Para problemas de regresión, la activación será la identidad `\(y_k = a_k\)`.
* Para clasificación binaria (output es una probabilidad) la activación será la sigmoide `\(y_k = \sigma(a_k)\)`.
* Para clasificación multiclase, usaremos la softmax.
`\begin{equation}
\text{softmax}(a)_i = \frac{e^{a_i}}{\sum_k e^{a_k}}
\end{equation}`
---
## Perceptrón multicapa (5)
* ¿Funciones de activación de capas intermedias?
* Históricamente, la sigmoide.
* Hoy en día, las más conocidas son la *REctifier Linear Unit (RELU)*, tangente hiperbólica y variantes.
<center>

</center>
---
## Perceptrón multicapa (6)
* Componiendo lo visto, obtenemos una NN de dos capas (e.g. con salida binarias)
`\begin{equation}
y(w,x) = \sigma \left( \sum_{j=0}^M w_{j}^{(2)} h \left( \sum_{i=0}^D w_{ji}^{(1)} x_i\right) \right)
\end{equation}`
* El proceso de evaluar esta función se denomina *forward propagation*.
.center[

[Fuente](https://victorzhou.com/blog/intro-to-neural-networks/)
]
---
## Perceptrón multicapa (7)
* Gráficamente...
<center>

</center>
---
class: middle, center, inverse
# Perceptrón multicapa - Entrenamiento
---
## Entrenamiento de la red
* Para entrenar, necesitamos definir función objetivo (función de coste).
* Una opción: **mínimos cuadrados**.
* Si damos **interpretación probabilística** a la salida de la NN, conseguimos una visión más general.
---
## Regresión
* Asumiremos que el target `\(t\)` sigue una distribución normal
`\begin{equation}
p(t \vert y(x,w), \beta^{-1})
\end{equation}`
* Donde la activación de la capa de salida es la identidad.
* Dado conjunto de entrenamiento `\(X = \lbrace x_1, \dots, x_N \rbrace\)`, `\(\boldsymbol{t} = t_1, \dots, t_N\)`, maximizar la verosimilitud es equivalente a
`\begin{equation}
w_{ML} = \arg\min_w E(w) = \arg\min_w \frac{1}{2} \sum_{i=1}^N \lbrace y(x_n,w) - t_n\rbrace^2
\end{equation}`
* Ojo: la **no linealidad** de la red hace que `\(E(w)\)` no sea convexo... en la práctica conseguiremos converger a mínimo local.
* En regresión multi-target, se asume **independencia condicional** de los targets dados `\(x\)` y `\(w\)` y el análisis es idéntico.
---
## Clasificación binaria
* `\(t=1\)` representa una pertenencia a una clase y `\(t=0\)` a la otra. La NN tiene una única salida con activación sigmoide.
* Interpretamos `\(y(x,w)\)` como `\(p(t=1 \vert x )\)`. Entonces
`\begin{equation}
p(t \vert x,w) = y(x,w)^t \lbrace 1-y(x,w) \rbrace^{1-t}
\end{equation}`
* Dado conjunto de entrenamiento, maximizar la verosimilitud equivale a minimizar la **entropía cruzada**
`\begin{equation}
E(w) = - \sum_{n=1}^N \lbrace t_n \log y_n + (1-t_n) \log (1-y_n) \rbrace
\end{equation}`
* Para clasificación binaria **multi-etiqueta**, usamos una red con `\(K\)` outputs sigmoidales.
* Asumiendo independencia condiciones de las etiquetas dado el input, el análisis es idéntico.
---
## Clasificación multiclase
* Las `\(K\)` posibles clases se escriben en notación One-Hot-Encoding.
* Si la observación `\(n\)`-ésima, pertenece a la clase 1, entonces `\(t_{n1}=1\)` y `\(t_{nj} = 0\)` para `\(j \neq 1\)`.
* La red tiene `\(K\)` salidas interpretadas como `\(y_k(x,w) = p(t_{\cdot k} = 1 \vert x)\)`.
* Maximizar la verosimilitud equivale a minimizar
`\begin{equation}
E(w) = - \sum_{n=1}^N \sum_{k=1}^K t_{nk} \log y_k(x_n,w)
\end{equation}`
* La red tiene `\(K\)` unidades de salida con activación softmax.
---
## Optimización
* Una vez definida la función de coste, hay que encontrar los pesos que la optimicen.
* `\(\nabla E(w) = 0\)` no se puede resolver analíticamente. Tenemos que usar métodos numéricos iterativos.
* Los más importantes: **basados en el gradiente**, pues como veremos, evaluar el gradiente es muy eficiente gracias al algoritmo de *backpropagation*.
* Descenso por el gradiente requiere inicializar los pesos e iterar:
`\begin{equation}
w^{t+1} = w^t - \eta \nabla E(w^t)
\end{equation}`
* En cada iteración, accedemos a todos los datos para calcular `\(\nabla E(w^t)\dots\)` complejidad `\(\mathcal{O}(N)\)`.
---
## Descenso por el gradiente estocástico (SGD)
* La función de coste tiene esta forma:
`\begin{equation*}
E(w) = \sum_{i=1}^N E_i(w)
\end{equation*}`
--
* En cada iteración, escogemos **un dato** al azar
`\begin{equation*}
w^{t+1} = w^t - \eta_t \nabla_w E_i(w^t)
\end{equation*}`
---
## Descenso por el gradiente estocástico (SGD)
* También podemos seleccionar un **minilote** `\(\mathcal{B}\)`
`\begin{equation*}
w^{t+1} = w^t - \eta_t \nabla_w \frac{1}{B} \sum_{i \in \mathcal{B}} f_i(w^t)
\end{equation*}`
* La complejidad pasa de `\(\mathcal{O}(N)\)` a `\(\mathcal{O}(B)\)`, además, no es necesario tener toda la matriz `\(X\)`, sino solo los datos del minilote `\(\mathcal{B}\)`.
* Otra ventaja: mayor probabilidad de escapar óptimos locales que con GD, un punto estacionario de la función objetivo en GD no lo será en SGD generalmente.
---
## Descenso por el gradiente estocástico (SGD)
* Usando resultados de aproximación estocástica de Robbins & Monro (1954), se puede demostrar convergencia a mínimo local siempre y cuando
1. Las tasas de aprendizaje cumplen estas condiciones:
`\begin{align*}
\sum_{t=0}^\infty \eta_t &= \infty \\
\sum_{t=0}^\infty \eta^2_t &< \infty
\end{align*}`
2. El gradiente que se utiliza en cada iteración es un estimador **no sesgado** del gradiente.
---
## Eecto de la estocasticidad

---
## Nuevos desarrollos
* **Momento (1986)**
Ayuda a amortiguar las oscilaciones que hacen que SGD sea lento.
`\begin{align*}
w^{t+1} &= w^t - v^{t+1} \\
v^{t+1} &= \gamma v^{t} + \eta_t \nabla_w E_i(w^t)
\end{align*}`
* **AdaGrad (2011)**
Adapta la tasa de aprendizaje a cada parámetro, disminuyéndola en parámetros con actualizaciones frecuentes (resp. aumentándola en parámetros con actualizaciones infrecuentes).
`\begin{equation*}
w^{t+1}_j = w^t_j - \frac{\eta}{\sqrt{G^t_{j,j} + \epsilon}} \nabla_w E_i(w^t)_j
\end{equation*}`
donde `\(G^t_{j,j} = \sum_{t'=0}^t (\nabla_w f_i(w^t)_j)^2\)` (la suma de los gradientes al cuadrado para esa coordenada hasta `\(t\)`)
---
## Nuevos desarrollos
* **RMSProp**
Adapta la tasa de aprendizaje dividiéndola por una media del cuadrado de los gradientes anteriores, que decae exponencialmente.
* **Adam**, evolución de AdaGrad.
* Muchos más...
* Una revisión de los diferentes optimizadores puede encontrarse en
[aqui](http://ruder.io/optimizing-gradient-descent/index.html#rmsprop).
---
class: middle, center, inverse
# Perceptrón muilticapa. Backpropagation
---
## Backpropagation (1)
* Técnica **eficiente** para evaluar `\(\nabla E(w)\)` aprovechando la estructura de perceptrones multicapa.
* En mayoría de problemas `\(E(w) = \sum_n E_n (w)\)`, nos centramos en evaluar `\(\nabla E_n(w)\)`.
* En un MLP, cada unidad calcula combinación lineal de sus inputs `\(z_i\)`, `\(a_j = \sum_i w_{ji}z_i\)`.
* Como output devuelve `\(z_j = h(a_j)\)`.
--
* Supongamos que para cada instancia the train, hemos calculado inputs y outputs de todas las neuronas (*forward propagation*).
* Evaluamos la derivada de `\(E_n\)` respecto `\(w_{ji}\)`
`\begin{equation}
\frac{\partial E_n}{\partial w_{ji}} = \frac{\partial E_n}{\partial a_j} \frac{\partial a_j}{\partial w_{ji}} := \delta_j z_i
\end{equation}`
* Donde `\(\delta_j = \frac{\partial E_n}{\partial a_j}\)`.
---
## Backpropagation (2)
* Para calcular las derivadas, únicamente necesitamos calcular `\(\delta_j\)` para cada unidad.
* Para cualquier unidad oculta, `\(E_n\)` es función de `\(a_j\)`, únicamente a través de las `\(a_k\)` de la capa siguiente.
`\begin{equation}
\delta_j = \frac{\partial E_n}{\partial a_j} = \sum_k \frac{\partial E_n}{\partial a_k} \frac{\partial a_k}{\partial a_{j}}
\end{equation}`
<center>

</center>
---
## Backpropagation (2)
* Efectuando las derivadas vemos que
`\begin{equation}
\delta_j = h'(a_j) \sum_k w_{kj} \delta_k
\end{equation}`
* Para unidad de salida calcular `\(\delta_j\)` es trivial, e.g. `\(E_n = \frac{1}{2} (y_n - t_n)^2\)`, y la activación es la identidad, entonces
`\begin{equation}
\delta = y_n - t_n
\end{equation}`
---
## Backpropagation (3)
* El algoritmo
1. Meter vector `\(x_n\)` a la red y realizar el *forward pass* de la red, para calcular inputs y outputs en cada unidad.
2. Evaluar `\(\delta\)` en la unidad de salida.
3. Propagar las `\(\delta\)`'s hacia atrás para obtener `\(\delta_j\)` en cada unidad usando
`\begin{equation}
\delta_j = h'(a_j) \sum_k w_{kj} \delta_k
\end{equation}`
4. Evaluar las derivadas usando
`\begin{equation}
\frac{\partial E_n}{\partial w_{ji}} = \delta_j z_i
\end{equation}`
---
## Backpropagation (4)
* Aspecto crucial de *backpropagation* es su eficiencia.
* Sea `\(W\)` el número totad de pesos.
* Calcular el gradiente usando *backpropagation*, requiere `\(O(W)\)` operaciones, para `\(W\)` suficientemente grande.
* Esto es así, pues el número de pesos suele ser mucho mayor que el número de neuronas.
* Esto implica que el cuello de botella en la computación es evaluar las combinaciones lineales. La evaluación de las activaciones requiere menos carga, pues hay tantas activaciones como neuronas.
---
## Backpropagation (5)
* **Ejercicio**: ¿Cuál es la complejidad de evaluar la derivada usando diferencias centrales?
`\begin{equation}
\frac{\partial E_n}{\partial w_{ji}} = \frac{E_n(w_{ji} + \epsilon) - E_n(w_{ji} - \epsilon)}{2 \epsilon} + O(\epsilon^2)
\end{equation}`
---
class: middle, center, inverse
# Perceptrón multicapa. Regularización
---
## Regularización (1)
* Número de unidades de input y output se eligen teniendo en cuenta la dimensionalida de los datos.
* Número de unidades ocultas `\(M\)`, es un hiperparámetro que regula la complejidad del modelo.
* Existirá un valor óptimo que equilibre entre underfitting y overfitting.
* Alternativa: escoger `\(M\)` lo suficientemente grande, y añadir regularizadores:
1. L2: `\(\lambda\Vert w \Vert_2^2\)`, conocido como *weight decay*.
2. L1: `\(\lambda \Vert w \Vert_1\)`
---
## Regularización (2)
* Otra alternativa es usar *early stopping*.
* Como entrenamos de forma iterativa, podemos observar el comportamiento de una estimación del error de generalización mientras vamos entrenando.
* Guardamos un conjunto de validación, y en cada época, calculamos el error producido en este conjunto de validación.
* Observaremos que el error primero decrece, y después, cuando se hace overfitting, crece.
* Dejaremos de entrenar antes de que esto último suceda.
* Esto, en algunos casos, es equivalente a reducir la complejidad efectiva de la red.
---
## Regularización (3)
* Otra alternativa es usar *dropout*.
* En cada ejemplo de cada iteración del entrenamiento, "apagar" cada neurona con probabilidad `\(1-p\)`.
* En cada iteración se entrena una red de tamaño efectivo menor.
<center>

</center>
---
class: middle, center, inverse
# Redes Neuronales Bayesianas
---
## ¿Por qué BNNs?
* **Cuantifican la incertidumbre** en los pesos.
* **Cuantifican la incertidumbre** en la salida de la red.
* Permiten la selección directa de **hiperparámetros**, sin necesidad de validación.
* Previenen overfitting, y que la respuesta de la red es un "promedio" sobre muchas redes (cada una pesada con la distribución a posteriori).
`\begin{equation}
p(t \vert \mathcal{D}, x) = \int p(t \vert w, x) p(w \vert \mathcal{D}) dw
\end{equation}`
---
## ¿Por qué no BNNs?
* La dependencia **altamente no lineal** de la salida con los pesos, hace que la inferencia Bayesiana exact sea inviable.
* Métodos MCMC no escalan bien.
* Alternativas:
1. Versiones sofisticadas de MCMC, por ejemplo <a href="https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf">esto</a>.
2. Inferencia variacional: aproximar el posterior por una gaussiana multivariante (mean-field o full rank).
* Campo activo de investigación!
</textarea>
<style data-target="print-only">@media screen {.remark-slide-container{display:block;}.remark-slide-scaler{box-shadow:none;}}</style>
<script src="https://remarkjs.com/downloads/remark-latest.min.js"></script>
<script src="macros.js"></script>
<script>var slideshow = remark.create({
"highlightStyle": "github",
"highlightLines": true,
"countIncrementalSlides": false
});
if (window.HTMLWidgets) slideshow.on('afterShowSlide', function (slide) {
window.dispatchEvent(new Event('resize'));
});
(function(d) {
var s = d.createElement("style"), r = d.querySelector(".remark-slide-scaler");
if (!r) return;
s.type = "text/css"; s.innerHTML = "@page {size: " + r.style.width + " " + r.style.height +"; }";
d.head.appendChild(s);
})(document);
(function(d) {
var el = d.getElementsByClassName("remark-slides-area");
if (!el) return;
var slide, slides = slideshow.getSlides(), els = el[0].children;
for (var i = 1; i < slides.length; i++) {
slide = slides[i];
if (slide.properties.continued === "true" || slide.properties.count === "false") {
els[i - 1].className += ' has-continuation';
}
}
var s = d.createElement("style");
s.type = "text/css"; s.innerHTML = "@media print { .has-continuation { display: none; } }";
d.head.appendChild(s);
})(document);
// delete the temporary CSS (for displaying all slides initially) when the user
// starts to view slides
(function() {
var deleted = false;
slideshow.on('beforeShowSlide', function(slide) {
if (deleted) return;
var sheets = document.styleSheets, node;
for (var i = 0; i < sheets.length; i++) {
node = sheets[i].ownerNode;
if (node.dataset["target"] !== "print-only") continue;
node.parentNode.removeChild(node);
}
deleted = true;
});
})();</script>
<script>
(function() {
var links = document.getElementsByTagName('a');
for (var i = 0; i < links.length; i++) {
if (/^(https?:)?\/\//.test(links[i].getAttribute('href'))) {
links[i].target = '_blank';
}
}
})();
</script>
<script>
slideshow._releaseMath = function(el) {
var i, text, code, codes = el.getElementsByTagName('code');
for (i = 0; i < codes.length;) {
code = codes[i];
if (code.parentNode.tagName !== 'PRE' && code.childElementCount === 0) {
text = code.textContent;
if (/^\\\((.|\s)+\\\)$/.test(text) || /^\\\[(.|\s)+\\\]$/.test(text) ||
/^\$\$(.|\s)+\$\$$/.test(text) ||
/^\\begin\{([^}]+)\}(.|\s)+\\end\{[^}]+\}$/.test(text)) {
code.outerHTML = code.innerHTML; // remove <code></code>
continue;
}
}
i++;
}
};
slideshow._releaseMath(document);
</script>
<!-- dynamically load mathjax for compatibility with self-contained -->
<script>
(function () {
var script = document.createElement('script');
script.type = 'text/javascript';
script.src = 'https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-MML-AM_CHTML';
if (location.protocol !== 'file:' && /^https?:/.test(script.src))
script.src = script.src.replace(/^https?:/, '');
document.getElementsByTagName('head')[0].appendChild(script);
})();
</script>
</body>
</html>