栈的特点是后入先出
根据这个特点可以临时保存一些数据,之后用到依次再弹出来,常用于 DFS 深度搜索
队列一般常用于 BFS 广度搜索,类似一层一层的搜索
设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。
思路:用两个栈实现,一个最小栈始终保证最小值在顶部
class MinStack {
private:
stack<int> normalStack;
stack<int> min_stack;
public:
/** initialize your data structure here. */
MinStack() {
min_stack.push(INT_MAX);
}
void push(int x) {
normalStack.push(x);
min_stack.push(min(min_stack.top(), x));
}
void pop() {
normalStack.pop();
min_stack.pop();
}
int top() {
return normalStack.top();
}
int getMin() {
return min_stack.top();
}
};evaluate-reverse-polish-notation
波兰表达式计算 > 输入: ["2", "1", "+", "3", "*"] > 输出: 9 解释: ((2 + 1) * 3) = 9
思路:通过栈保存原来的元素,遇到表达式弹出运算,再推入结果,重复这个过程
int evalRPN(vector<string>& tokens) {
if(tokens.size() == 0) return 0;
stack<int> res;
for(string s : tokens){
if(s != "+" && s != "-" && s != "*" && s != "/"){
res.push(stoi(s));
}else{
// 注意:a为被除数,b为除数
int b = res.top(); res.pop();
int a = res.top(); res.pop();
if(s == "+") res.push(a + b);
if(s == "-") res.push(a - b);
if(s == "*") res.push(a * b);
if(s == "/") res.push(a / b);
}
}
return res.top();
}给定一个经过编码的字符串,返回它解码后的字符串。 s = "3[a]2[bc]", 返回 "aaabcbc". s = "3[a2[c]]", 返回 "accaccacc". s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".
思路:通过栈辅助进行操作
string decodeString(string s) {
string res;
int num = 0;
stack<int> stackInt;
stack<string> stackStr;
for(char c : s){
if(c == '['){
stackInt.push(num);
num = 0;
stackStr.push(res);
res = "";
}else if(c == ']'){
int times = stackInt.top();
stackInt.pop();
for(int i = 0; i < times; i++){
stackStr.top() += res;
}
res = stackStr.top();
stackStr.pop();
}else if(c >= '0' && c <= '9'){
num = num * 10 + c - '0';
}else{
res = res + c;
}
}
return res;
}利用栈进行 DFS 递归搜索模板
boolean DFS(int root, int target) {
Set<Node> visited;
Stack<Node> s;
add root to s;
while (s is not empty) {
Node cur = the top element in s;
return true if cur is target;
for (Node next : the neighbors of cur) {
if (next is not in visited) {
add next to s;
add next to visited;
}
}
remove cur from s;
}
return false;
}给定一个二叉树,返回它的中序遍历。
// 思路:通过stack 保存已经访问的元素,用于原路返回
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if(root == NULL) return res;
stack<TreeNode *> s;
s.push(root);
while(!s.empty()){
TreeNode *t = s.top();
s.pop();
if(t != NULL){
if(t->right) s.push(t->right);
s.push(t);
s.push(NULL);
if(t->left) s.push(t->left);
}else{
res.push_back(s.top()->val);
s.pop();
}
}
return res;
}给你无向连通图中一个节点的引用,请你返回该图的深拷贝(克隆)。
unordered_map<Node*, Node*> mp;
Node* cloneGraph(Node* node) {
if(node == NULL) return node;
if(mp.count(node)) return mp[node];
const auto newNode = new Node(node->val);
mp[node] = newNode;
for(auto n : node->neighbors){
mp[node]->neighbors.push_back(cloneGraph(n));
}
return mp[node];
}给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
思路:通过深度搜索遍历可能性(注意标记已访问元素)
int numIslands(vector<vector<char>>& grid) {
int count = 0;
for(int i = 0; i < grid.size(); i++){
for(int j = 0; j < grid[0].size(); j++){
if(grid[i][j] == '1'){
dfs(grid, i, j);
count++;
}
}
}
return count;
}
void dfs(vector<vector<char>>& grid, int i, int j){
if(i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] != '1'){
return;
}
grid[i][j] = '2';
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
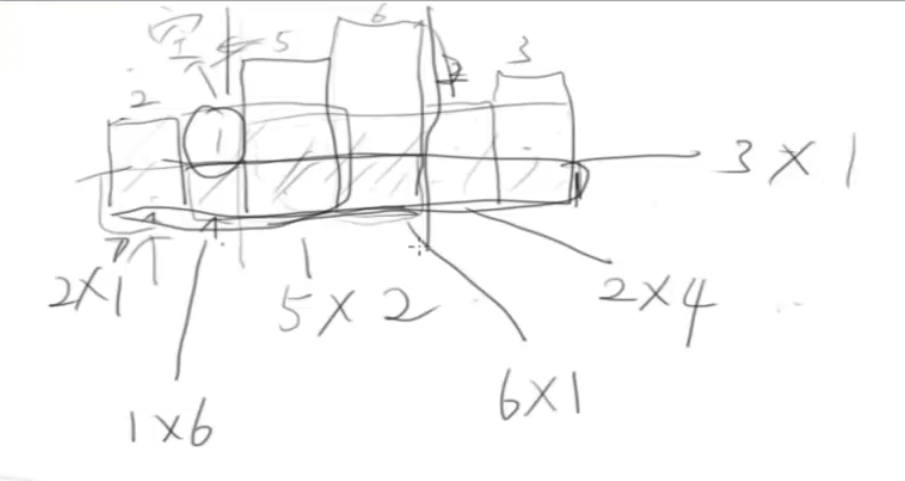
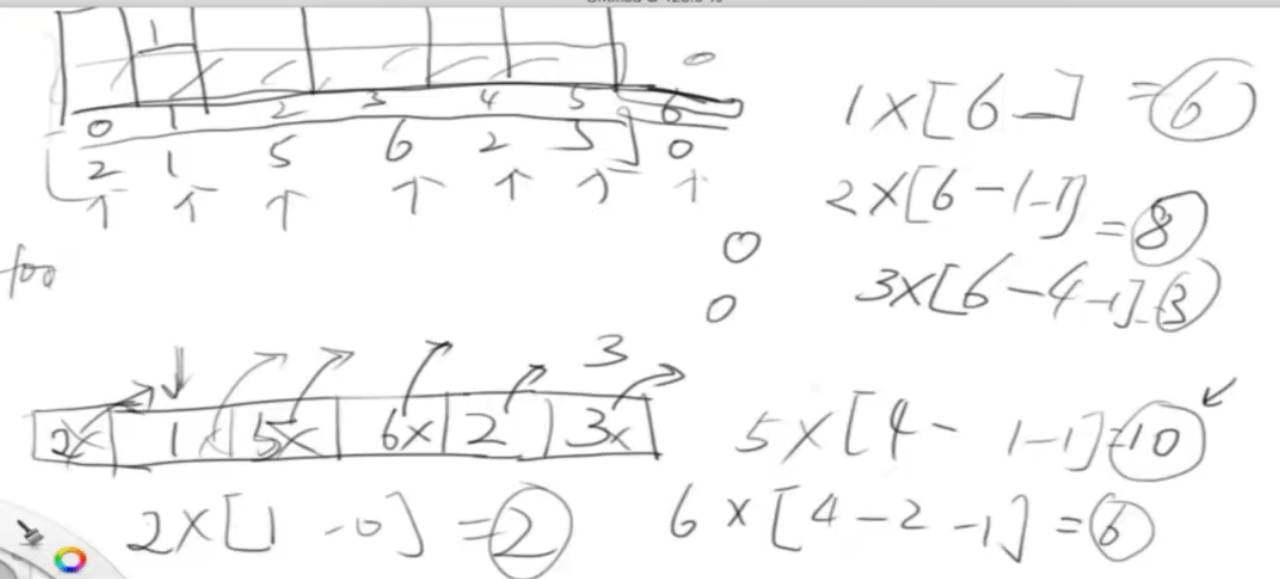
}largest-rectangle-in-histogram
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。
思路:求以当前柱子为高度的面积,即转化为寻找小于当前值的左右两边值
用栈保存小于当前值的左的元素
int largestRectangleArea(vector<int>& heights) {
//基于各个高度的最大矩形是在出栈的时候计算的,因此必须要让所有高度都出栈。
//这里是利用单调栈的性质让其全部出栈,即在原始数组后添一个0
heights.push_back(0);
stack<int> s;
int maxArea = 0;
for(int i = 0; i < heights.size(); i++){
while(!s.empty() && heights[i] < heights[s.top()]){
int h = heights[s.top()];
s.pop();
int w = s.empty() ? i : i - s.top() - 1;
maxArea = max(maxArea, h * w);
}
s.push(i);
}
return maxArea;
}常用于 BFS 宽度优先搜索
使用栈实现队列
class MyQueue {
public:
stack<int> inStack;
stack<int> outStack;
/** Initialize your data structure here. */
MyQueue() {
}
/** Push element x to the back of queue. */
void push(int x) {
inStack.push(x);
}
/** Removes the element from in front of queue and returns that element. */
int pop() {
cheak();
int top = outStack.top();
outStack.pop();
return top;
}
/** Get the front element. */
int peek() {
cheak();
return outStack.top();
}
/** Returns whether the queue is empty. */
bool empty() {
return inStack.empty() && outStack.empty();
}
void cheak(){
if(outStack.empty()){
while(!inStack.empty()){
outStack.push(inStack.top());
inStack.pop();
}
}
}
};二叉树层次遍历
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if(root == NULL) return res;
queue<TreeNode *> q;
q.push(root);
while(!q.empty()){
int size = q.size();
res.push_back(vector<int>());
for(int i = 0; i < size; i++){
TreeNode *t = q.front();
res.back().push_back(t->val);
q.pop();
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
}
return res;
}给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。 两个相邻元素间的距离为 1
// BFS 从0进队列,弹出之后计算上下左右的结果,将上下左右重新进队列进行二层操作
// 0 0 0 0
// 0 x 0 0
// x x x 0
// 0 x 0 0
// 0 0 0 0
// 0 1 0 0
// 1 x 1 0
// 0 1 0 0
// 0 0 0 0
// 0 1 0 0
// 1 2 1 0
// 0 1 0 0
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int r = matrix.size(), c = matrix[0].size();
vector<pair<int, int>> directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
vector<vector<int>> res(r, vector<int>(c, INT_MAX));
queue<pair<int, int>> q;
for(int i = 0; i < r; i++){
for(int j = 0; j < c; j++){
if(matrix[i][j] == 0){
res[i][j] = 0;
q.push({i, j});
}
}
}
while(!q.empty()){
auto temp = q.front();
q.pop();
for(int i = 0; i < 4; i++){
int x = temp.first + directions[i].first;
int y = temp.second + directions[i].second;
if(x >= 0 && x < r && y >= 0 && y < c){
if(res[x][y] > res[temp.first][temp.second] + 1){
res[x][y] = res[temp.first][temp.second] + 1;
q.push({x, y});
}
}
}
}
return res;
}- 熟悉栈的使用场景
- 后入先出,保存临时值
- 利用栈 DFS 深度搜索
- 熟悉队列的使用场景
- 利用队列 BFS 广度搜索