1091

1091. Shortest Path in Binary Matrix (Medium)

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

• All the visited cells of the path are 0.
• All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

 

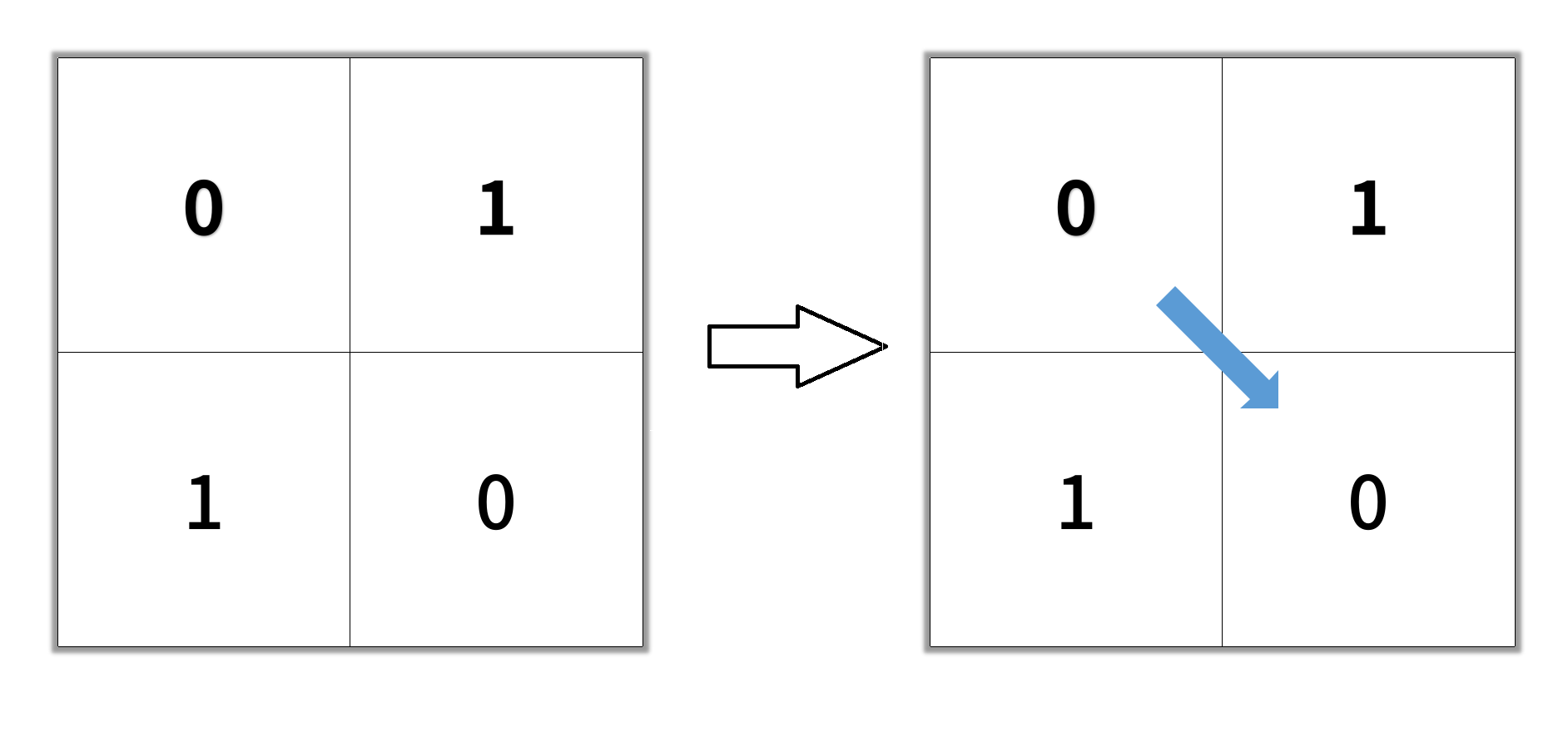
Example 1:

Input: grid = [[0,1],[1,0]]
Output: 2

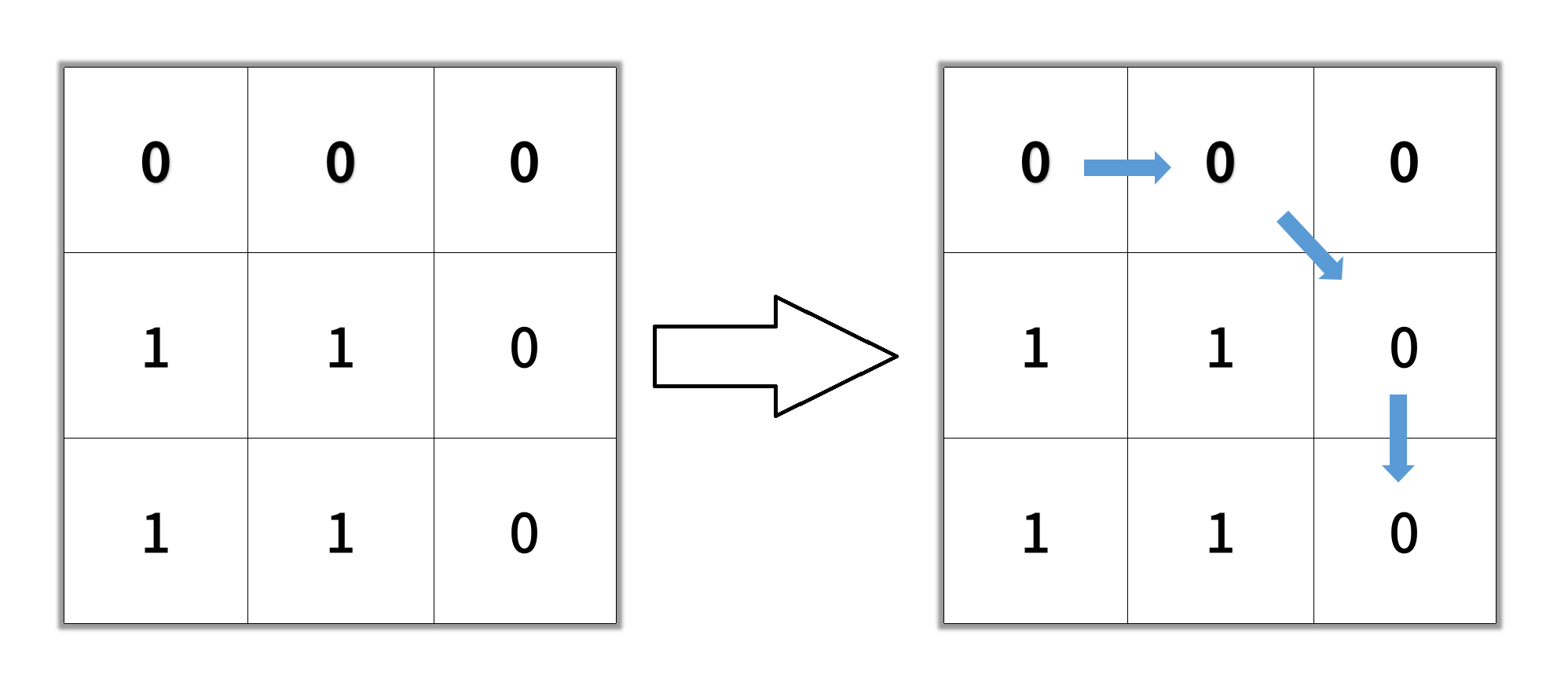
Example 2:

Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

 

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] is 0 or 1

Related Topics:
Array, Breadth-First Search, Matrix

Solution 1. BFS

// OJ: https://leetcode.com/problems/shortest-path-in-binary-matrix/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N^2)
class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& G) {
        if (G[0][0] == 1) return -1;
        int N = G.size();
        vector<vector<int>> dist(N, vector<int>(N, INT_MAX));
        queue<pair<int, int>> q;
        q.emplace(0, 0);
        dist[0][0] = 1;
        while (q.size()) {
            auto [x, y] = q.front();
            q.pop();
            for (int dx = -1; dx <= 1; ++dx) {
                for (int dy = -1; dy <= 1; ++dy) {
                    if (dx == 0 && dy == 0) continue;
                    int a = x + dx, b = y + dy;
                    if (a < 0 || a >= N || b < 0 || b >= N || G[a][b] == 1 || dist[a][b] != INT_MAX) continue;
                    dist[a][b] = dist[x][y] + 1;
                    q.emplace(a, b);
                }
            }
        }
        return dist[N - 1][N - 1] == INT_MAX ? -1 : dist[N - 1][N - 1];
    }
};

Or

// OJ: https://leetcode.com/problems/shortest-path-in-binary-matrix/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N) for elements in the queue
class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& A) {
        if (A[0][0]) return -1;
        int N = A.size(), ans = 1;
        queue<pair<int, int>> q{{{0,0}}};
        while (q.size()) {
            int cnt = q.size();
            while (cnt--) {
                auto [x, y] = q.front();
                q.pop();
                if (x == N - 1 && y == N - 1) return ans;
                for (int dx = -1; dx <= 1; ++dx) {
                    for (int dy = -1; dy <= 1; ++dy) {
                        if (dx == 0 && dy == 0) continue;
                        int a = x + dx, b = y + dy;
                        if (a < 0 || b < 0 || a >= N || b >= N || A[a][b]) continue;
                        A[a][b] = 1;
                        q.emplace(a, b);
                    }
                }
            }
            ++ans;
        }
        return -1;
    }
};