1368

1368. Minimum Cost to Make at Least One Valid Path in a Grid (Hard)

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

 

Example 1:

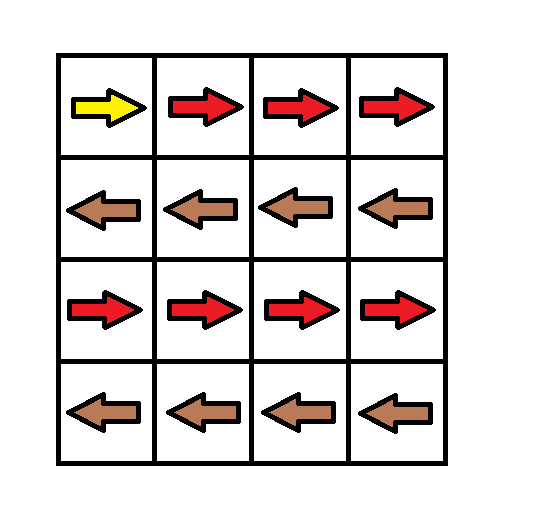
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

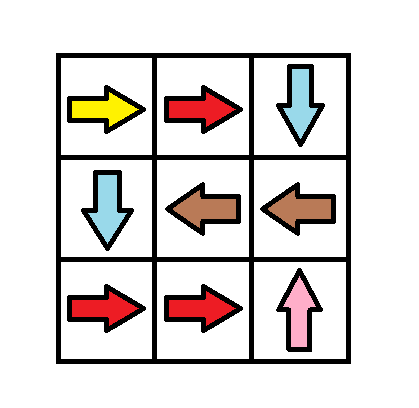
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

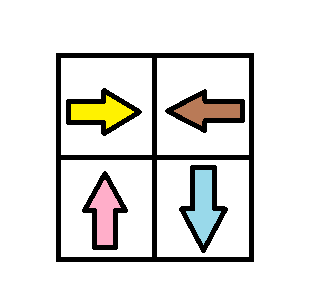
Input: grid = [[1,2],[4,3]]
Output: 1

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• 1 <= grid[i][j] <= 4

Companies:
Google

Related Topics:
Array, Breadth-First Search, Graph, Heap (Priority Queue), Matrix, Shortest Path

Similar Questions:

• Minimum Weighted Subgraph With the Required Paths (Hard)

Solution 1. BFS + DP

// OJ: https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(MN)
class Solution {
public:
    int minCost(vector<vector<int>>& G) {
        int M = G.size(), N = G[0].size(), dp[100][100] = {}, dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
        memset(dp, 0x3f, sizeof(dp));
        dp[0][0] = 0;
        queue<pair<int, int>> q{{{0, 0}}};
        while (q.size()) {
            auto [x, y] = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                int a = x + dirs[i][0], b = y + dirs[i][1];
                if (a < 0 || b < 0 || a >= M || b >= N) continue;
                int cost = dp[x][y] + (G[x][y] - 1 != i);
                if (dp[a][b] > cost) {
                    dp[a][b] = cost;
                    q.emplace(a, b);
                }
            }
        }
        return dp[M - 1][N - 1];
    }
};

Solution 2. Dijkstra

// OJ: https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/
// Author: github.com/lzl124631x
// Time: O(MNlogMN)
// Space: O(MN)
class Solution {
public:
    int minCost(vector<vector<int>>& G) {
        int M = G.size(), N = G[0].size(), dist[100][100] = {}, dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
        memset(dist, 0x3f, sizeof(dist));
        dist[0][0] = 0;
        priority_queue<array<int, 3>, vector<array<int, 3>>, greater<>> pq;
        pq.push({ 0, 0, 0 });
        while (pq.size()) {
            auto [d, x, y] = pq.top();
            pq.pop();
            if (d > dist[x][y]) continue;
            if (x == M - 1 && y == N - 1) return d;
            for (int i = 0; i < 4; ++i) {
                int a = x + dirs[i][0], b = y + dirs[i][1];
                if (a < 0 || a >= M || b < 0 || b >= N) continue;
                int cost = d + (G[x][y] - 1 != i);
                if (cost < dist[a][b]) {
                    dist[a][b] = cost;
                    pq.push({ cost, a, b });
                }
            }
        }
        return 0;
    }
};