1453

1453. Maximum Number of Darts Inside of a Circular Dartboard (Hard)

You have a very large square wall and a circular dartboard placed on the wall. You have been challenged to throw darts into the board blindfolded. Darts thrown at the wall are represented as an array of points on a 2D plane. 

Return the maximum number of points that are within or lie on any circular dartboard of radius r.

 

Example 1:

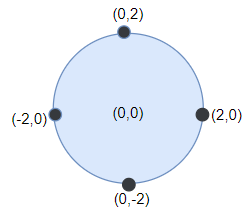
Input: points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
Output: 4
Explanation: Circle dartboard with center in (0,0) and radius = 2 contain all points.

Example 2:

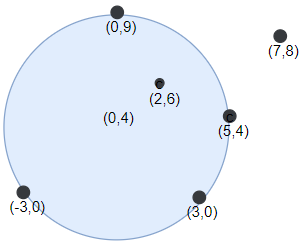
Input: points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
Output: 5
Explanation: Circle dartboard with center in (0,4) and radius = 5 contain all points except the point (7,8).

Example 3:

Input: points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
Output: 1

Example 4:

Input: points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
Output: 4

 

Constraints:

• 1 <= points.length <= 100
• points[i].length == 2
• -10^4 <= points[i][0], points[i][1] <= 10^4
• 1 <= r <= 5000

Companies:
Facebook

Related Topics:
Array, Math, Geometry

Solution 1.

// OJ: https://leetcode.com/problems/maximum-number-of-darts-inside-of-a-circular-dartboard/
// Author: github.com/lzl124631x
// Time: O(N^3)
// Space: O(1)
class Solution {
    inline double dist(const vector<double> &a, const vector<double> &b) {
        return sqrt(pow(a[0] - b[0], 2) + pow(a[1] - b[1], 2));
    }
    vector<double> getPoint(const vector<double> &a, const vector<double> &b, double p, double q) {
        double x = (a[1] - b[1] + b[0] * q - a[0] * p) / (q - p);
        double y = a[1] + p * (x - a[0]);
        return {x, y};
    }
    vector<vector<double>> getCenters(const vector<double> &a, const vector<double> &b, int r) {
        double d = dist(a, b);
        if (d > 2 * r) return {};
        if (d == 2 * r) return {{ (a[0] + b[0]) / 2, (a[1] + b[1]) / 2 }};
        double theta = acos(d / 2 / r);
        double alpha = atan2(a[1] - b[1], a[0] - b[0]);
        double p = tan(alpha + theta), q = tan(alpha - theta);
        return { getPoint(a, b, p, q), getPoint(a, b, q, p) };
    }
public:
    int numPoints(vector<vector<int>>& A, int r) {
        int N = A.size(), ans = 0;
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                for (auto &center : getCenters({(double)A[i][0], (double)A[i][1]}, {(double)A[j][0], (double)A[j][1]}, r)) {
                    int cnt = 0;
                    for (auto &p : A) {
                        cnt += dist(center, {(double)p[0], (double)p[1]}) <= r + 0.00001;
                    }
                    ans = max(ans, cnt);
                }
            }
        }
        return ans;
    }
};

TODO

https://leetcode.com/problems/maximum-number-of-darts-inside-of-a-circular-dartboard/discuss/636372/JavaC%2B%2BPython-POJ-1981