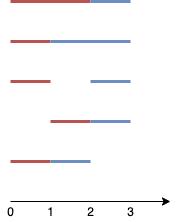Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.
Return the number of ways we can draw k non-overlapping line segments. Since this number can be huge, return it modulo 109 + 7.
Example 1:
Input: n = 4, k = 2
Output: 5
Explanation:
The two line segments are shown in red and blue.
The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.
Example 2:
Input: n = 3, k = 1
Output: 3
Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.
Example 3:
Input: n = 30, k = 7 Output: 796297179 Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.
Example 4:
Input: n = 5, k = 3 Output: 7
Example 5:
Input: n = 3, k = 2 Output: 1
Constraints:
2 <= n <= 10001 <= k <= n-1
Related Topics:
Recursion
Let dp[i][j] be the number of ways we can draw j segments using the first i points (0th to i-1th).
For dp[i][j], we have two options:
- The last segment doesn't end with
ith point. This providesdp[i-1][j]cases. - The last segment ends with
ith point. Then:
- If the last segment covers 2 points, there are
dp[i-1][j-1]cases. - If the last segment covers 3 points, there are
dp[i-2][j-1]cases. - ...
- If the last segment covers
ipoints, there aredp[1][j-1]cases.
So the 2nd case provides sum( dp[t][j-1] | 1 <= t <= i-1 ) cases in total.
Note that i points can only have i-1 segments. So to get j-1 segments, we at least need j points. So we can tighten the range of t to j <= t <= i-1.
So the 2nd case provides sum( dp[t][j-1] | j <= t <= i-1 ) cases in total.
Now we have the transition formula:
dp[i][j] = dp[i-1][j] + sum( dp[t][j-1] | j <= t <= i-1 )
Now condier the edge cases:
When i == 1, we only have a single point and can't form any segment, so dp[1][j] = 0.
When j == 0, we don't need to form any segment, so dp[i][0] = 1.
So in sum:
dp[i][j] = dp[i-1][j] + sum( dp[t][j-1] | j <= t <= i-1, 1 <= i <= N, 1 <= j <= K )
dp[1][j] = 0
dp[i][0] = 1
If we directly use this formula, the solution is as follows. However, this will get TLE.
// OJ: https://leetcode.com/problems/number-of-sets-of-k-non-overlapping-line-segments/
// Author: github.com/lzl124631x
// Time: O(N^2 * K)
// Space: O(NK)
// NOTE: this solution will get TLE
class Solution {
public:
int numberOfSets(int n, int k) {
long mod = 1e9+7;
vector<vector<long>> dp(n + 1, vector<long>(k + 1));
for (int i = 0; i < n; ++i) dp[i + 1][0] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= k; ++j) {
dp[i][j] = dp[i - 1][j];
for (int t = j; t <= i - 1; ++t) dp[i][j] = (dp[i][j] + dp[t][j - 1]) % mod;
}
}
return dp[n][k];
}
};It's inefficient because we recompute the sum part over and over again.
To avoid repetitive computation, we can use prefix sum:
dp[i][j] = dp[i-1][j] + presum(i-1, j-1)
where presum(i-1, j-1) = sum( dp[t][j-1] | 1 <= t <= i-1 )
// OJ: https://leetcode.com/problems/number-of-sets-of-k-non-overlapping-line-segments/
// Author: github.com/lzl124631x
// Time: O(NK)
// Space: O(NK)
class Solution {
public:
int numberOfSets(int n, int k) {
long mod = 1e9+7;
vector<long> presum(k + 1);
vector<vector<long>> dp(n + 1, vector<long>(k + 1));
for (int i = 0; i < n; ++i) dp[i + 1][0] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= k; ++j) {
presum[j - 1] = (presum[j - 1] + dp[i - 1][j - 1]) % mod;
dp[i][j] = (dp[i - 1][j] + presum[j - 1]) % mod;
}
}
return dp[n][k];
}
};Since in each iteration we only need dp[i-1][j-1] and dp[i][j-1], we can reduce the dp array from N * K to 1 * K.
// OJ: https://leetcode.com/problems/number-of-sets-of-k-non-overlapping-line-segments/
// Author: github.com/lzl124631x
// Time: O(NK)
// Space: O(K)
class Solution {
public:
int numberOfSets(int n, int k) {
long mod = 1e9+7;
vector<long> presum(k + 1);
vector<long> dp(k + 1);
dp[0] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = k; j >= 1; --j) {
presum[j - 1] = (presum[j - 1] + dp[j - 1]) % mod;
dp[j] = (dp[j] + presum[j - 1]) % mod;
}
}
return dp[k];
}
};Instead of using prefix sum, we can update the formula.
dp[i][j] = dp[i-1][j] + ( dp[1][j-1] + dp[2][j-1] + ... + dp[i-2][j-1] + dp[i-1][j-1] )
dp[i-1][j] = dp[i-2][j] + ( dp[1][j-1] + dp[2][j-1] + ... + dp[i-2][j-1] )
// So
dp[i][j] = 2 * dp[i-1][j] - dp[i-2][j] + dp[i-1][j-1] where 2 <= i <= N
// OJ: https://leetcode.com/problems/number-of-sets-of-k-non-overlapping-line-segments/
// Author: github.com/lzl124631x
// Time: O(NK)
// Space: O(NK)
class Solution {
public:
int numberOfSets(int n, int k) {
long mod = 1e9+7;
vector<vector<long>> dp(n + 1, vector<long>(k + 1));
for (int i = 1; i <= n; ++i) dp[i][0] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= k; ++j) {
dp[i][j] = (((dp[i - 1][j] * 2) % mod - dp[i - 2][j] + mod) % mod + dp[i - 1][j - 1]) % mod;
}
}
return dp[n][k];
}
};This problem is equivalent to "given n + k - 1 points, get k segments that don't share endpoints.
// OJ: https://leetcode.com/problems/number-of-sets-of-k-non-overlapping-line-segments/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O()
// Ref: https://leetcode.com/problems/number-of-sets-of-k-non-overlapping-line-segments/discuss/898727/C%2B%2B-O(n)-solution-explained-in-detail-using-Stars-and-Bars
const int mod = 1e9 + 7, mx = 2e3 + 10;
int fact[mx], inv[mx], invfact[mx];
int mult(int a, int b) { return (1LL * a * b) % mod; }
int comb(int n, int r) {
if (r > n) return 0;
return (1LL * fact[n] * invfact[n - r] % mod) * invfact[r] % mod;
}
class Solution {
void initInv() {
fact[0] = invfact[0] = fact[1] = invfact[1] = inv[1] = 1;
for (int i = 2; i < mx; ++i) {
fact[i] = mult(fact[i - 1], i);
inv[i] = mult(inv[mod % i], mod - mod / i);
invfact[i] = mult(invfact[i - 1], inv[i]);
}
}
public:
int numberOfSets(int n, int k) {
initInv();
return comb(n + k - 1, 2 * k);
}
};