You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.
Return the length of the longest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node.
Example 1:
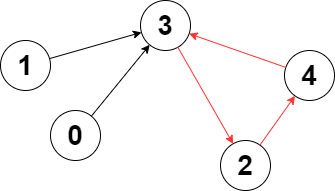
Input: edges = [3,3,4,2,3] Output: 3 Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2. The length of this cycle is 3, so 3 is returned.
Example 2:
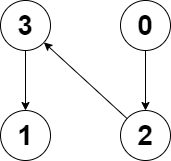
Input: edges = [2,-1,3,1] Output: -1 Explanation: There are no cycles in this graph.
Constraints:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
Related Topics:
Depth-First Search, Graph, Topological Sort
Similar Questions:
- Strange Printer II (Hard)
- Minimum Number of Operations to Sort a Binary Tree by Level (Medium)
- Shortest Cycle in a Graph (Hard)
- Similar to topological sort, keep removing nodes with 0 indegrees.
- For the remaining nodes, DFS to get the depth
// OJ: https://leetcode.com/problems/longest-cycle-in-a-graph
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
int longestCycle(vector<int>& E) {
int N = E.size(), ans = -1;
vector<int> indegree(N), depth(N);
for (int i = 0; i < N; ++i) {
if (E[i] == -1) continue;
indegree[E[i]]++;
}
queue<int> q;
for (int i = 0; i < N; ++i) {
if (indegree[i] == 0) q.push(i);
}
while (q.size()) {
int u = q.front();
q.pop();
depth[u] = -1; // depth[u] == -1 means that this node u is not in a cycle.
if (E[u] != -1 && --indegree[E[u]] == 0) q.push(E[u]);
}
function<int(int, int)> dfs = [&](int i, int d) {
if (depth[i] == -1) return -1;
depth[i] = d;
if (depth[E[i]]) return depth[i];
return depth[i] = dfs(E[i], 1 + d);
};
for (int i = 0; i < N; ++i) {
ans = max(ans, dfs(i, 1));
}
return ans;
}
};