You are given the root of a binary tree with unique values.
In one operation, you can choose any two nodes at the same level and swap their values.
Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
The level of a node is the number of edges along the path between it and the root node.
Example 1:
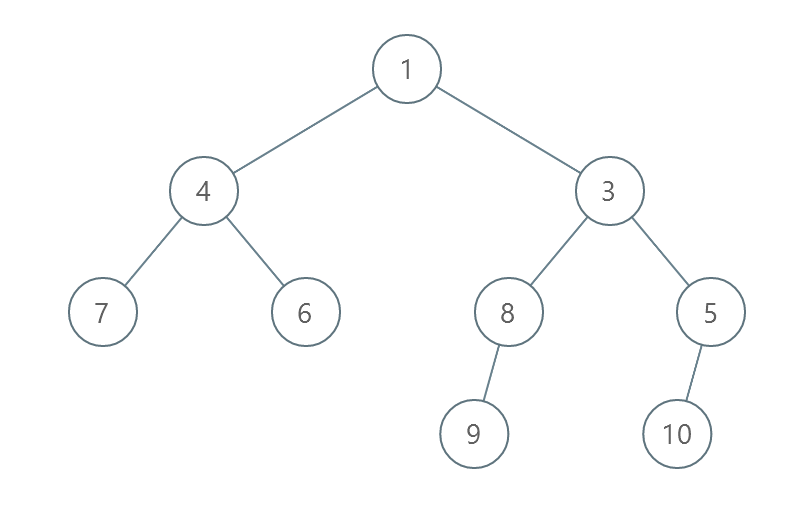
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10] Output: 3 Explanation: - Swap 4 and 3. The 2nd level becomes [3,4]. - Swap 7 and 5. The 3rd level becomes [5,6,8,7]. - Swap 8 and 7. The 3rd level becomes [5,6,7,8]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 2:
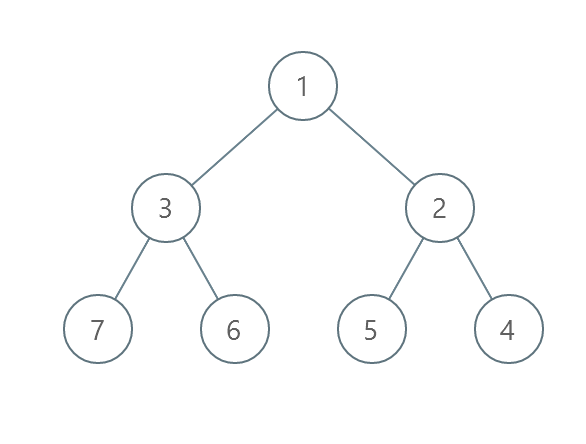
Input: root = [1,3,2,7,6,5,4] Output: 3 Explanation: - Swap 3 and 2. The 2nd level becomes [2,3]. - Swap 7 and 4. The 3rd level becomes [4,6,5,7]. - Swap 6 and 5. The 3rd level becomes [4,5,6,7]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 3:
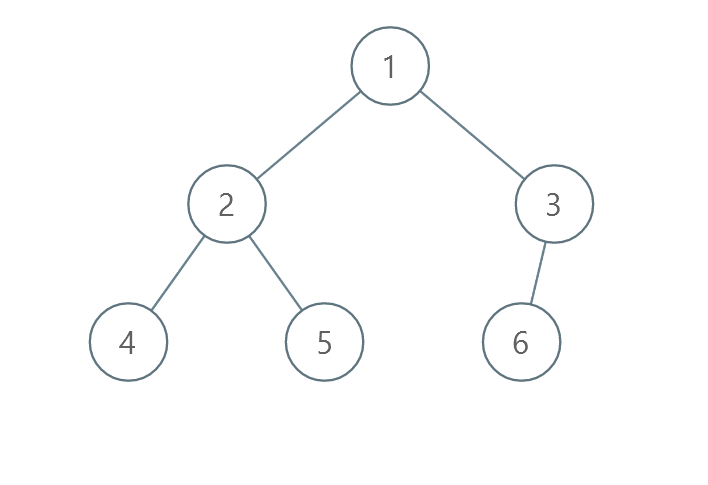
Input: root = [1,2,3,4,5,6] Output: 0 Explanation: Each level is already sorted in increasing order so return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- All the values of the tree are unique.
Companies: Amazon
Related Topics:
Tree, Breadth-First Search, Binary Tree
Similar Questions:
We collect the node values at each level. For a specific level, we count the minimum swaps to make that level ordered.
Assume the values at current level is A = [7,6,8,5], we create an index array id = [0,1,2,3] initially, and sort it based on the corresponding value in A.
After sorting, id = [3,1,0,2], meaning A[3]=5 is the smallest element, A[1]=6 is the next element, and so on.
Then we can rewrite A by setting A[id[i]] = i. Then, A = [2,1,3,0] and this normalizes the A to range [0, N-1].
Then, we just need to do swaps to make A[i] = i.
- For
i = 0,A[0] = 2 != 0, so we should swapA[0] = 2to its final index2. Then,A = [3,1,2,0]. - For
i = 0,A[0] = 3 != 0, so we should swapA[0] = 3to its final index3. Then,A = [0,1,2,3]. - Now,
A[i] = ifor all indices.
Now we just need to do swaps to make id[i] = i for each i.
// OJ: https://leetcode.com/problems/minimum-number-of-operations-to-sort-a-binary-tree-by-level
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(N)
class Solution {
public:
int minimumOperations(TreeNode* root) {
queue<TreeNode*> q{{root}};
int ans = 0;
while (q.size()) {
int cnt = q.size();
vector<int> v, id(cnt);
iota(begin(id), end(id), 0);
while (cnt--) {
auto n = q.front();
q.pop();
v.push_back(n->val);
if (n->left) q.push(n->left);
if (n->right) q.push(n->right);
}
sort(begin(id), end(id), [&](int a, int b) { return v[a] < v[b]; });
for (int i = 0; i < id.size(); ++i) v[id[i]] = i;
for (int i = 0; i < id.size(); ++i) {
while (v[i] != i) {
swap(v[v[i]], v[i]);
++ans;
}
}
}
return ans;
}
};This solution shows that we can also do this operation directly on id array. (But its explanation is wrong. A=[7,11,3,5,2]'s index array after sorting should be id=[4,2,3,0,1]).
Again, consider A=[7,6,8,5] and sorted index array id=[3,1,0,2]. id[3] = 2 means that A[2] = 8's correct index is 3. So, we should swap A[2] and A[3]. It is id[0] = 3 that represents A[3], so we should swap id[0] with id[2].
In this solution, instead of finding which id[i] = 3, it scans from the left id[0] = 3, find id[id[0]] = id[3] = 2, and swap id[0]=3 with id[3]=2, which effectively swaps A[3] with A[2].
// OJ: https://leetcode.com/problems/minimum-number-of-operations-to-sort-a-binary-tree-by-level
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(N)
class Solution {
public:
int minimumOperations(TreeNode* root) {
queue<TreeNode*> q{{root}};
int ans = 0;
while (q.size()) {
int cnt = q.size();
vector<int> v, id(cnt);
iota(begin(id), end(id), 0);
while (cnt--) {
auto n = q.front();
q.pop();
v.push_back(n->val);
if (n->left) q.push(n->left);
if (n->right) q.push(n->right);
}
sort(begin(id), end(id), [&](int a, int b) { return v[a] < v[b]; });
for (int i = 0; i < id.size(); ++i) {
while (id[i] != i) {
swap(id[i], id[id[i]]);
++ans;
}
}
}
return ans;
}
};