3123

3123. Find Edges in Shortest Paths (Hard)

You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.

Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.

Return the array answer.

Note that the graph may not be connected.

 

Example 1:

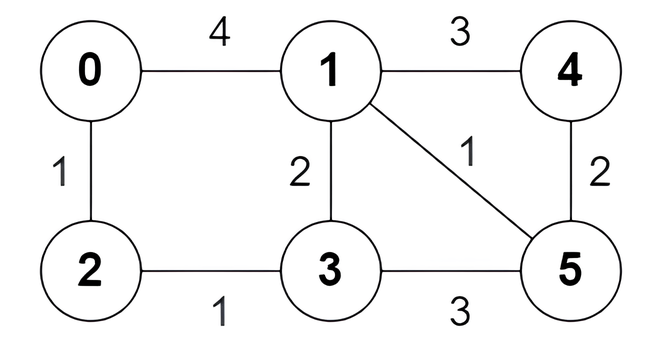
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

Output: [true,true,true,false,true,true,true,false]

Explanation:

The following are all the shortest paths between nodes 0 and 5:

• The path 0 -> 1 -> 5: The sum of weights is 4 + 1 = 5.
• The path 0 -> 2 -> 3 -> 5: The sum of weights is 1 + 1 + 3 = 5.
• The path 0 -> 2 -> 3 -> 1 -> 5: The sum of weights is 1 + 1 + 2 + 1 = 5.

Example 2:

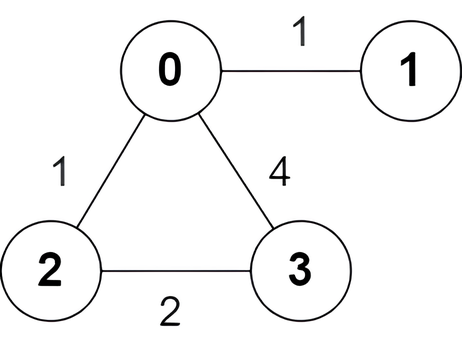
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

Output: [true,false,false,true]

Explanation:

There is one shortest path between nodes 0 and 3, which is the path 0 -> 2 -> 3 with the sum of weights 1 + 2 = 3.

 

Constraints:

• 2 <= n <= 5 * 104
• m == edges.length
• 1 <= m <= min(5 * 104, n * (n - 1) / 2)
• 0 <= ai, bi < n
• ai != bi
• 1 <= wi <= 105
• There are no repeated edges.

Hints:

• Find all the shortest paths starting from nodes 0 and n - 1 to all other nodes.
• How to use the above calculated shortest paths to check if an edge is part of at least one shortest path from 0 to n - 1?

Solution 1. Dijkstra

// OJ: https://leetcode.com/problems/find-edges-in-shortest-paths
// Author: github.com/lzl124631x
// Time: O(ElogE)
// Space: O(E)
typedef pair<int, int> PII;
class Solution {
public:
    vector<bool> findAnswer(int n, vector<vector<int>>& E) {
        vector<vector<PII>> G(n);
        for (auto &e : E) {
            int u = e[0], v = e[1], w = e[2];
            G[u].emplace_back(v, w);
            G[v].emplace_back(u, w);
        }
        auto dijkstra = [&](int source) {
            priority_queue<PII, vector<PII>, greater<PII>> pq;
            vector<int> dists(n, INT_MAX);
            dists[source] = 0;
            pq.emplace(0, source);
            while (pq.size()) {
                auto [cost, u] = pq.top();
                pq.pop();
                if (cost > dists[u]) continue;
                for (auto &[v, w] : G[u]) {
                    if (dists[v] > dists[u] + w) {
                        dists[v] = dists[u] + w;
                        pq.emplace(dists[v], v);
                    }
                }
            }
            return dists;
        };
        auto da = dijkstra(0), db = dijkstra(n - 1);
        int goal = da[n - 1];
        vector<bool> ans(E.size());
        if (goal >= INT_MAX) return ans;
        for (int i = 0; i < E.size(); ++i) {
            auto &e = E[i];
            int u = e[0], v = e[1], w = e[2];
            ans[i] = (da[u] + w + db[v] == goal || da[v] + w + db[u] == goal);
        }
        return ans;
    }
};