441

441. Arranging Coins (Easy)

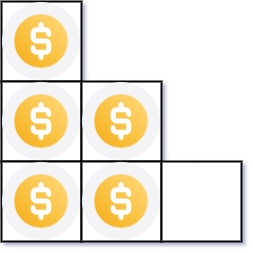
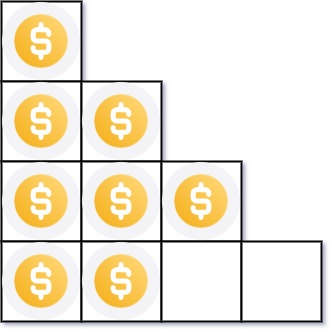
You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number of complete rows of the staircase you will build.

 

Example 1:

Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.

 

Constraints:

• 1 <= n <= 231 - 1

Companies:
Salesforce

Related Topics:
Math, Binary Search

Solution 1. Brute Force

// OJ: https://leetcode.com/problems/arranging-coins/
// Author: github.com/lzl124631x
// Time: O(sqrt(N))
// Space: O(1)
class Solution {
public:
    int arrangeCoins(int n) {
        long i = 1, sum = 0;
        while (sum + i <= n) sum += i++;
        return i - 1;
    }
};

Solution 2. Binary Search

// OJ: https://leetcode.com/problems/arranging-coins/
// Author: github.com/lzl124631x
// Time: O(logN)
// Space: O(1)
class Solution {
public:
    int arrangeCoins(int n) {
        int L = 1, R = n;
        while (L <= R) {
            long M = L + (R - L) / 2, sum = M * (1 + M) / 2;
            if (sum == n) return M;
            if (sum < n) L = M + 1;
            else R = M - 1;
        }
        return R;
    }
};

Or use L < R

// OJ: https://leetcode.com/problems/arranging-coins/
// Author: github.com/lzl124631x
// Time: O(logN)
// Space: O(1)
class Solution {
public:
    int arrangeCoins(int n) {
        int L = 1, R = n;
        while (L < R) {
            long M = R - (R - L) / 2, sum = M * (1 + M) / 2;
            if (sum <= n) L = M;
            else R = M - 1;
        }
        return L;
    }
};

Solution 3. Math

x * (x + 1) / 2 <= n

x^2 + x - 2n <= 0

x <= (sqrt(8n + 1) - 1) / 2

// OJ: https://leetcode.com/problems/arranging-coins/
// Author: github.com/lzl124631x
// Time: O(1)
// Space: O(1)
class Solution {
public:
    int arrangeCoins(int n) {
        return (sqrt((long)8 * n + 1) - 1) / 2;
    }
};