There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered 0, 1, and 2.
The square room has walls of length p, and a laser ray from the southwest corner first meets the east wall at a distance q from the 0th receptor.
Return the number of the receptor that the ray meets first. (It is guaranteed that the ray will meet a receptor eventually.)
Example 1:
Input: p = 2, q = 1 Output: 2 Explanation: The ray meets receptor 2 the first time it gets reflected back to the left wall.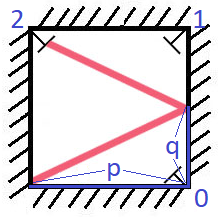
Note:
1 <= p <= 10000 <= q <= p
Related Topics:
Math
The equation of the ray is (y - y1) / ry = (x - x1) / rx.
We start from x = 0, y = 0 and rx = p, ry = q.
After time t the ray will be at (a, b) = (x + rx * t, y + ry * t). We want to find the smallest positive t which makes (a, b) be at (0, p), (p, 0) or (p, p).
At time t, if the ray lands on
- the west edge, then
x + rx * t = 0sot = -x / rx. - the south edge, then
y + ry * t = 0, sot = -y / ry. - the east edge, then
x + rx * t = p, sot = (p - x) / rx. - the north edge, then
y + ry * t = p, sot = (p - y) / ry.
We can try the four edges, and the smallest positive time t is the time we should take because it takes us to the next landing edge.
// OJ: https://leetcode.com/problems/mirror-reflection/
// Author: github.com/lzl124631x
// Time: O(P)
// Space: O(1)
// Ref: https://leetcode.com/problems/mirror-reflection/solution/
class Solution {
double eps = 1e-6;
bool equal(double x, double y) {
return abs(x - y) < eps;
}
public:
int mirrorReflection(int p, int q) {
double x = 0, y = 0, rx = p, ry = q;
while (!(
(equal(x, p) && (equal(y, 0) || equal(y, p))) // touches 0 or 1
|| (equal(x, 0) && equal(y, p)) // touches 2
)) {
double t = 1e9;
if ((-x / rx) > eps) t = min(t, -x / rx); // try reaching west edge (set the new x to be 0)
if ((-y / ry) > eps) t = min(t, -y / ry); // try reaching south edge (set the new y to be 0)
if ((p - x) / rx > eps) t = min(t, (p - x) / rx); // try reaching east edge (set the new x to be p)
if ((p - y) / ry > eps) t = min(t, (p - y) / ry); // try reaching north edge (set the new y to be p)
x += rx * t; // we take the closest reacheable edge
y += ry * t;
if (equal(x, p) || equal(x, 0)) rx *= -1; // if touches west or east edge, flip rx
else ry *= -1; // otherwise flip ry.
}
if (equal(x, p) && equal(y, p)) return 1;
return equal(x, p) ? 0 : 2;
}
};Instead of bounceing back, just let the ray go straight. The first receptor the ray touches is at (kp, kq) where k is integer and kq is a multiple of p. So the goal is the find the smallest integer k for which kq is a multiple of p.
The mathematical answer is k = p / gcd(p, q).
p /= k and q /= k reduces p and q to the base cases where p and q are coprime. For example, p = 9, q = 6 is reduced to p = 3, q = 2.
Then p and q won't be both even otherwise they are not coprime.
So we just have 3 cases:
p and q are
- odd, odd
- odd, even
- even, odd
respectively
Each case has a fixed top-right value as shown in the figure below.
So the pattern is:
pis odd andqis odd the result is1.pis odd andqis even, the result is0.pis even andqis odd, the result is2.
// OJ: https://leetcode.com/problems/mirror-reflection/
// Author: github.com/lzl124631x
// Time: O(logP)
// Space: O(1)
// Ref: https://leetcode.com/problems/mirror-reflection/solution/
class Solution {
int gcd(int p, int q) {
return q ? gcd(q, p % q) : p;
}
public:
int mirrorReflection(int p, int q) {
int k = gcd(p, q);
p /= k; p %= 2;
q /= k; q %= 2;
if (p == 1 && q == 1) return 1;
return p == 1 ? 0 : 2;
}
};Similar to Solution 2, but we don't need to compute the GCD. Simply keep dividing p and q by 2 until they are not both even. Then we use the parity of p and q to determine the result.
// OJ: https://leetcode.com/problems/mirror-reflection/
// Author: github.com/lzl124631x
// Time: O(logP)
// Space: O(1)
// Ref: https://leetcode.com/problems/mirror-reflection/discuss/141765/Java-short-solution-with-a-sample-drawing
class Solution {
public:
int mirrorReflection(int p, int q) {
while (p % 2 == 0 && q % 2 == 0) p /= 2, q /= 2;
if (p % 2 && q % 2) return 1;
return p % 2 ? 0 : 2;
}
};Or
// OJ: https://leetcode.com/problems/mirror-reflection/
// Author: github.com/lzl124631x
// Time: O(logP)
// Space: O(1)
class Solution {
public:
int mirrorReflection(int p, int q) {
while (p % 2 == 0 && q % 2 == 0) p /= 2, q /= 2;
return 1 + (q & 1) - (p & 1);
}
};
