959

959. Regions Cut By Slashes (Medium)

In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space.  These characters divide the square into contiguous regions.

(Note that backslash characters are escaped, so a \ is represented as "\\".)

Return the number of regions.

 

Example 1:

Input:
[
  " /",
  "/ "
]
Output: 2
Explanation: The 2x2 grid is as follows: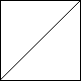

Example 2:

Input:
[
  " /",
  "  "
]
Output: 1
Explanation: The 2x2 grid is as follows: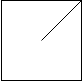

Example 3:

Input:
[
  "\\/",
  "/\\"
]
Output: 4
Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)
The 2x2 grid is as follows: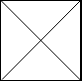

Example 4:

Input:
[
  "/\\",
  "\\/"
]
Output: 5
Explanation: (Recall that because \ characters are escaped, "/\\" refers to /\, and "\\/" refers to \/.)
The 2x2 grid is as follows:

Example 5:

Input:
[
  "//",
  "/ "
]
Output: 3
Explanation: The 2x2 grid is as follows:

 

Note:

1. 1 <= grid.length == grid[0].length <= 30
2. grid[i][j] is either '/', '\', or ' '.

Companies:
Uber

Related Topics:
Depth-first Search, Union Find, Graph

Solution 1. Union Find

Split each cell to 4 parts, top/right/bottom/left indexed by 0/1/2/3.

For each cell:

• If it's ' ', connect all 4 sub-cells
• If it's '/', connect top-left and bottom-right.
• If it's '\', connect top-right and bottom-left.
• Connect the 4 sub-cells with the neighboring sub-cells. For example, connect the top sub-cell with the bottom sub-cell of the cell above.

// OJ: https://leetcode.com/problems/regions-cut-by-slashes
// Author: github.com/lzl124631x
// Time: O(N^2 * log(N^2))
// Space: O(N^2)
class UnionFind {
    vector<int> id;
    int cnt;
public:
    UnionFind(int n) : id(n), cnt(n) {
        iota(begin(id), end(id), 0);
    }
    int find(int a) {
        return id[a] == a ? a : (id[a] = find(id[a]));
    }
    void connect(int a, int b) {
        int x = find(a), y = find(b);
        if (x == y) return;
        id[x] = y;
        --cnt;
    }
    int getCount() { return cnt; }
};;
class Solution {
public:
    int regionsBySlashes(vector<string>& A) {
        int N = A.size(), dirs[4][2] = {{-1,0}, {0,1}, {1,0},{0,-1}}; // TRBL 0123
        UnionFind uf(4 * N * N);
        auto key = [&](int x, int y, int dir) { return 4 * (x * N + y) + dir; };
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                if (A[i][j] == ' ') {
                    for (int k = 1; k < 4; ++k) uf.connect(key(i, j, 0), key(i, j, k));
                } else if (A[i][j] == '/') {
                    uf.connect(key(i, j, 0), key(i, j, 3));
                    uf.connect(key(i, j, 1), key(i, j, 2));
                } else {
                    uf.connect(key(i, j, 0), key(i, j, 1));
                    uf.connect(key(i, j, 2), key(i, j, 3));
                }
                for (int k = 0; k < 4; ++k) {
                    auto &[dx, dy] = dirs[k];
                    int a = i + dx, b = j + dy;
                    if (a < 0 || a >= N || b < 0 || b >= N) continue;
                    uf.connect(key(i, j, k), key(a, b, (k + 2) % 4));
                }
            }
        }
        return uf.getCount();
    }
};