声明:本文为作者学习,自定义View系列教程的笔记,自定义View是由GcsSloop原创,它的GitHub地址为:https://github.com/GcsSloop
教程地址为:https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/%5B06%5DPath_Bezier.md
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
贝塞尔曲线于1962,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发,以稳定数值的方法求出贝兹曲线。
以上内容从采取自百度百科
贝塞尔曲线目前被广泛应用于计算机制图中,可以说贝塞尔曲线奠定了计算机制图的基础。
Android中绘制Path常用方法:
以下方法转载至GcsSloop的自定义View系列教程:https://github.com/GcsSloop/AndroidNote/tree/master/CustomView/README.md
| 作用 | 相关方法 | 备注 |
|---|---|---|
| 移动起点 | moveTo | 移动下一次操作的起点位置 |
| 设置终点 | setLastPoint | 重置当前path中最后一个点位置,如果在绘制之前调用,效果和moveTo相同 |
| 连接直线 | lineTo | 添加上一个点到当前点之间的直线到Path |
| 闭合路径 | close | 连接第一个点连接到最后一个点,形成一个闭合区域 |
| 添加内容 | addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo | 添加(矩形, 圆角矩形, 椭圆, 圆, 路径, 圆弧) 到当前Path (注意addArc和arcTo的区别) |
| 是否为空 | isEmpty | 判断Path是否为空 |
| 是否为矩形 | isRect | 判断path是否是一个矩形 |
| 替换路径 | set | 用新的路径替换到当前路径所有内容 |
| 偏移路径 | offset | 对当前路径之前的操作进行偏移(不会影响之后的操作) |
| 贝塞尔曲线 | quadTo, cubicTo | 分别为二次和三次贝塞尔曲线的方法 |
| rXxx方法 | rMoveTo, rLineTo, rQuadTo, rCubicTo | 不带r的方法是基于原点的坐标系(偏移量), rXxx方法是基于当前点坐标系(偏移量) |
| 填充模式 | setFillType, getFillType, isInverseFillType, toggleInverseFillType | 设置,获取,判断和切换填充模式 |
| 提示方法 | incReserve | 提示Path还有多少个点等待加入**(这个方法貌似会让Path优化存储结构)** |
| 布尔操作(API19) | op | 对两个Path进行布尔运算(即取交集、并集等操作) |
| 计算边界 | computeBounds | 计算Path的边界 |
| 重置路径 | reset, rewind | 清除Path中的内容 reset不保留内部数据结构,但会保留FillType. rewind会保留内部的数据结构,但不保留FillType |
| 矩阵操作 | transform | 矩阵变换 |
贝塞尔曲线应用简单场景:
- QQ小红点拖拽效果
- 平滑的折线图的制作
- 阅读软件的翻书效果
一阶贝塞尔曲线的原理就是一条直线,其实就是直接画了一个Path出来,在这里不做过多的介绍,本文主要介绍的是二阶的贝塞尔曲线。
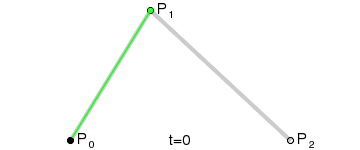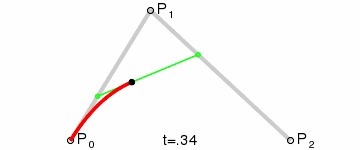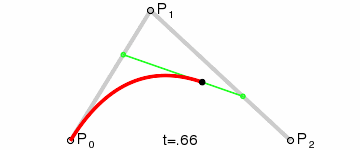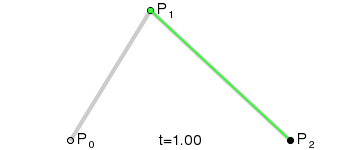
二阶贝塞尔曲线效果图:
二阶曲线由两个数据点(A 和 C),一个控制点(B)来描述曲线状态,大致如下:
上图中红色曲线部分就是传说中的二阶贝塞尔曲线,那么这条红色曲线是如何生成的呢?接下来我们就以其中的一个状态分析一下:
连接AB BC,并在AB上取点D,BC上取点E,使其满足条件:
连接DE,取点F,使得:
AD/AB = BE/BC = DF/DE
这样获取到的点F就是贝塞尔曲线上的一个点,动态过程如下:
public class Bezier2 extends View {
private Paint mPaint;
private int centerX, centerY;
private PointF start, end, control;
public Bezier2(Context context) {
super(context);
mPaint = new Paint();
mPaint.setColor(Color.BLACK);
mPaint.setStrokeWidth(8);
mPaint.setStyle(Paint.Style.STROKE);
mPaint.setTextSize(60);
start = new PointF(0,0);
end = new PointF(0,0);
control = new PointF(0,0);
}
public Bezier2(Context context, @Nullable AttributeSet attrs) {
super(context, attrs);
mPaint = new Paint();
mPaint.setColor(Color.BLACK);
mPaint.setStrokeWidth(8);
mPaint.setStyle(Paint.Style.STROKE);
mPaint.setTextSize(60);
start = new PointF(0,0);
end = new PointF(0,0);
control = new PointF(0,0);
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
centerX = w/2;
centerY = h/2;
// 初始化数据点和控制点的位置
start.x = centerX-200;
start.y = centerY;
end.x = centerX+200;
end.y = centerY;
control.x = centerX;
control.y = centerY-100;
}
@Override
public boolean onTouchEvent(MotionEvent event) {
// 根据触摸位置更新控制点,并提示重绘
control.x = event.getX();
control.y = event.getY();
invalidate();
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
// 绘制数据点和控制点
mPaint.setColor(Color.GRAY);
mPaint.setStrokeWidth(20);
canvas.drawPoint(start.x,start.y,mPaint);
canvas.drawPoint(end.x,end.y,mPaint);
canvas.drawPoint(control.x,control.y,mPaint);
// 绘制辅助线
mPaint.setStrokeWidth(4);
canvas.drawLine(start.x,start.y,control.x,control.y,mPaint);
canvas.drawLine(end.x,end.y,control.x,control.y,mPaint);
// 绘制贝塞尔曲线
mPaint.setColor(Color.RED);
mPaint.setStrokeWidth(8);
Path path = new Path();
path.moveTo(start.x,start.y);
path.quadTo(control.x,control.y,end.x,end.y);
canvas.drawPath(path, mPaint);
}
}代码地址:https://github.com/linsir6/mCustomView/tree/master/Bezier