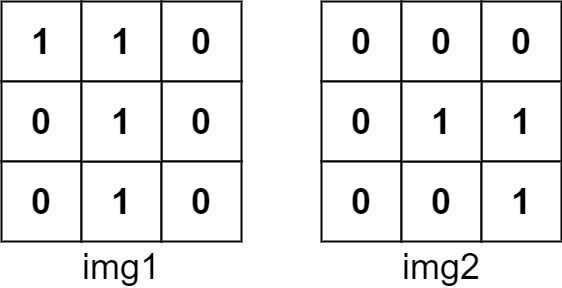
You are given two images img1 and img2 both of size n x n, represented as binary, square matrices of the same size. (A binary matrix has only 0s and 1s as values.)
We translate one image however we choose (sliding it left, right, up, or down any number of units), and place it on top of the other image. After, the overlap of this translation is the number of positions that have a 1 in both images.
(Note also that a translation does not include any kind of rotation.)
What is the largest possible overlap?
Example 1:
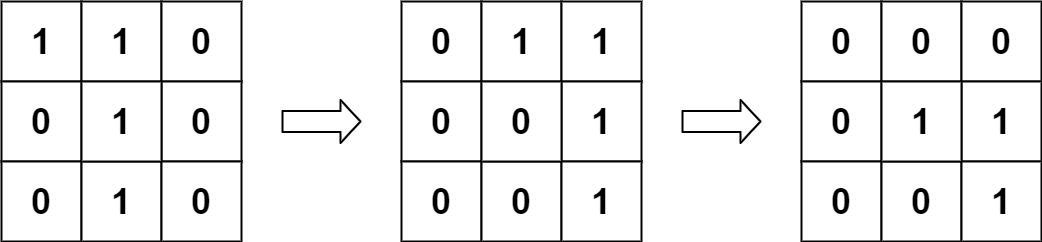
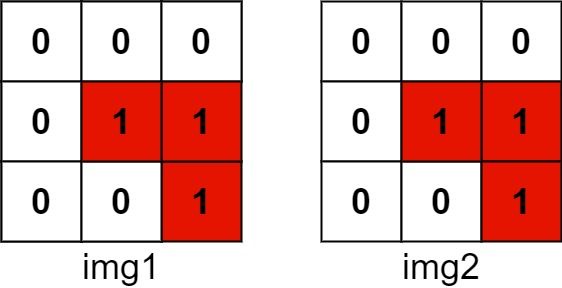
Input: img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]] Output: 3 Explanation: We slide img1 to right by 1 unit and down by 1 unit.The number of positions that have a 1 in both images is 3. (Shown in red)
Example 2:
Input: img1 = [[1]], img2 = [[1]] Output: 1
Example 3:
Input: img1 = [[0]], img2 = [[0]] Output: 0
Constraints:
n == img1.lengthn == img1[i].lengthn == img2.lengthn == img2[i].length1 <= n <= 30img1[i][j]is0or1.img2[i][j]is0or1.