A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
Given a row x col grid of integers, how many 3 x 3 "magic square" subgrids are there? (Each subgrid is contiguous).
Example 1:
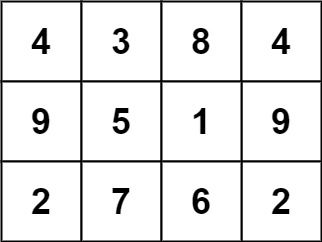
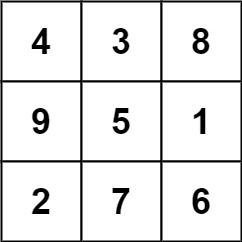
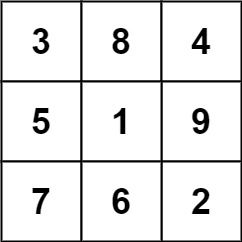
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]] Output: 1 Explanation: The following subgrid is a 3 x 3 magic square:while this one is not:
In total, there is only one magic square inside the given grid.
Example 2:
Input: grid = [[8]] Output: 0
Example 3:
Input: grid = [[4,4],[3,3]] Output: 0
Example 4:
Input: grid = [[4,7,8],[9,5,1],[2,3,6]] Output: 0
Constraints:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100 <= grid[i][j] <= 15