README.md

1548. 图中最相似的路径

English Version

题目描述

我们有 n 座城市和 m 条双向道路 roads ，其中 roads[i] = [ai, bi] 连接城市 ai 和城市 bi。每个城市有一个正好 3 个大写字母的名字，在数组 names中给出。从任意城市 x 出发，你可以到达任意城市 y ，其中 y != x （即：城市和道路形成一张无向连通图）。

给定一个字符串数组 targetPath，你需要找出图中与 targetPath 的 长度相同 且 编辑距离最小 的路径。

你需要返回 编辑距离最小的路径中节点的顺序 。该路径应当与 targetPath 的长度相等，且路径需有效（即： ans[i] 和 ans[i + 1] 间应存在直接连通的道路）。如果有多个答案，返回任意一个。

编辑距离 的定义如下：

define editDistance(targetPath, myPath) {
    dis := 0
    a := targetPath.length
    b := myPath.length
    if a != b {
        return 1000000000
    }
    for (i := 0; i < a; i += 1) {
        if targetPath[i] != myPath[i] {
            dis += 1
        }
    }
    return dis
}

 

进阶：如果路径中每个节点只可访问一次，你该如何修改你的答案？

 

示例 1：

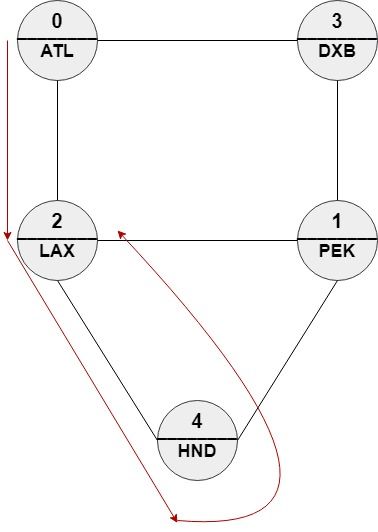
输入：n = 5, roads = [[0,2],[0,3],[1,2],[1,3],[1,4],[2,4]], names = ["ATL","PEK","LAX","DXB","HND"], targetPath = ["ATL","DXB","HND","LAX"]
输出：[0,2,4,2]
解释：[0,2,4,2], [0,3,0,2] 和 [0,3,1,2] 都是正确答案。
[0,2,4,2] 等价于 ["ATL","LAX","HND","LAX"] ，与 targetPath 的编辑距离 = 1。
[0,3,0,2] 等价于 ["ATL","DXB","ATL","LAX"] ，与 targetPath 的编辑距离 = 1。
[0,3,1,2] 等价于 ["ATL","DXB","PEK","LAX"] ，与 targetPath 的编辑距离 = 1。

示例 2：

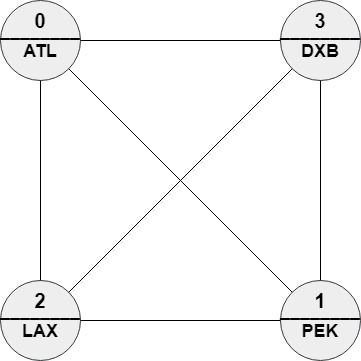
输入：n = 4, roads = [[1,0],[2,0],[3,0],[2,1],[3,1],[3,2]], names = ["ATL","PEK","LAX","DXB"], targetPath = ["ABC","DEF","GHI","JKL","MNO","PQR","STU","VWX"]
输出：[0,1,0,1,0,1,0,1]
解释：任意路径与 targetPath 的编辑距离都等于 8。

示例 3：

输入：n = 6, roads = [[0,1],[1,2],[2,3],[3,4],[4,5]], names = ["ATL","PEK","LAX","ATL","DXB","HND"], targetPath = ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]
输出：[3,4,5,4,3,2,1]
解释：[3,4,5,4,3,2,1] 是唯一与 targetPath 的编辑距离 = 0 的路径。
该路径等价于 ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]

 

提示：

• 2 <= n <= 100
• m == roads.length
• n - 1 <= m <= (n * (n - 1) / 2)
• 0 <= ai, bi <= n - 1
• ai != bi 
• 给定的图保证是连通的，任意两个节点至多有一个直接连通的道路。
• names.length == n
• names[i].length == 3
• names[i] 包含大写英文字母。
• 可能有两个名称相同的城市。
• 1 <= targetPath.length <= 100
• targetPath[i].length == 3
• targetPath[i] 由大写英文字母组成。

解法

Python3

Java

...