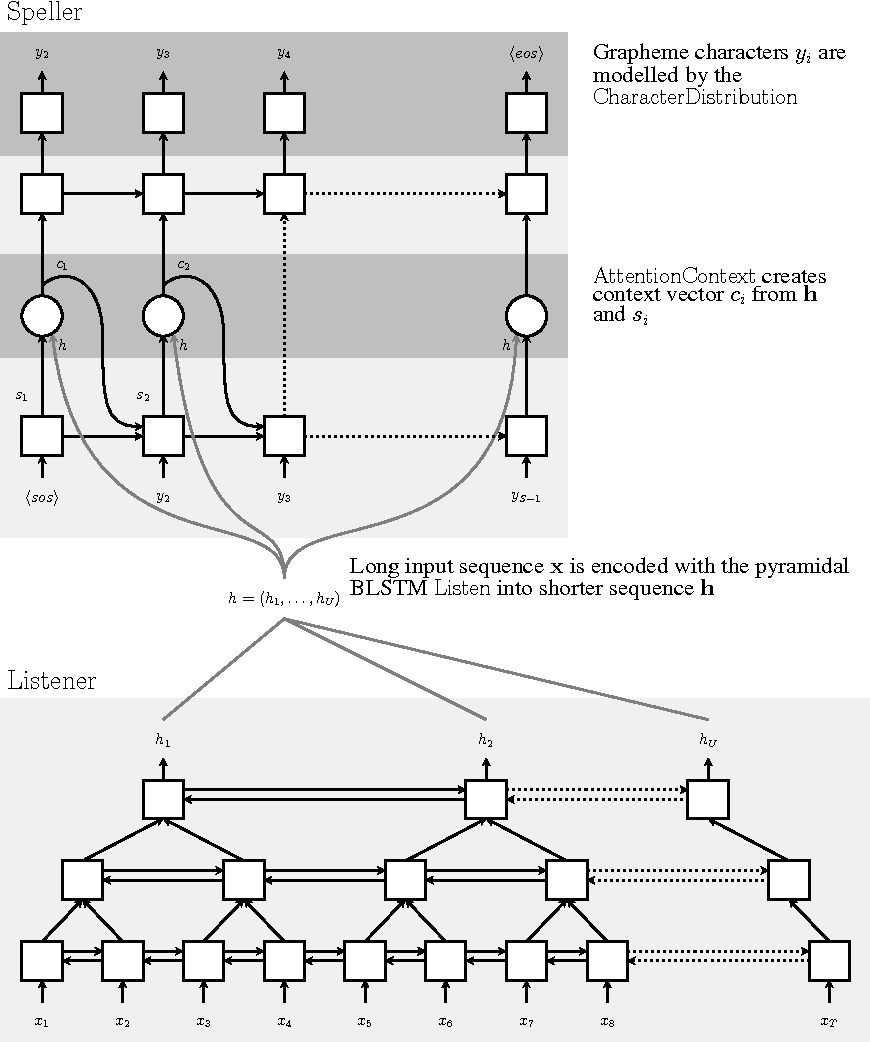
The Listen-Attend-Spell Model Listen-Attend-Spell (LAS) is a deep learning model that achieved better results than the RNN+CTC model .
CTC couples the input lengths with the output lengths. RNN-transducers avoids this unrealistic assumption.
A transducer consists of an encoder and a decoder. LAS is an RNN-transducer.
The encoder (listener) is a pyramidal bi-directional LSTM (pBLSTM):
Each output of the pBLSTM spans over a longer distance in the input sequence.
Simplifies the computational cost.
$$ h_i^j = \text{pBLSTM} \left(
h_{i-1}^j,
\left[ h_{2i}^{j-1}, h_{2i+1}^{j-1} \right]
\right) $$
The decoder attends and spells.
$$ s_i = \text{RNN}(s_{i-1}, y_{i-1}, c_{i-1}) $$
$$ c_i = \text{AttentionContext}(s_i, \mathbf{h}) $$
$$ P(y_i \mid \mathbf{x}, \mathbf{y}_{<i}) = \text{CharacterDistribution}(s_i, c_i) $$
The attention is represented by $\alpha_{i,u}$ , the distribution over $U$ :
$$ c_i = \sum_u \alpha_{i,u} h_u $$
$$ \alpha_{i,u} = \frac{ \exp(z_{i,u}) }{ \sum_u \exp(z_{i,u}) } $$
$$ z_{i,u} = \langle \phi(s_i), \psi(h_u) \rangle = \sum_k \phi_{i,k} \psi_{u,k} $$
Suppose that
$$ \phi(s_i) = \phi_i = W \cdot s_i $$
$$ \psi(h_u) = \psi_u = U \cdot h_u $$
Let us first make sure about the tensor-dimensions of our variables.
$s_i$ could be a vector, say, $A$ -dimensional
$h_u$ could be a vector, say, $B$ -dimensional; thus $\mathbf{h}$ is $U\times B$ .
$W$ and $U$ must project the $s_i$ and $h_u$ to the same lengths, so could we compute the inner-product in the new $K$ -dimensional space, so
$\phi_i$ is $K$ -dimensional
$\psi_u$ is $K$ -dimensional
$W$ is $K \times A$
$U$ is $K \times B$
$\alpha_{i,u}$ and $z_{i,u}$ are scalar values.
$c_i$ is a blend of $h_u$ over $u$ , so it has the same dimension as $h_u$ , or, $B$ .
During the backpropagation, given $\frac{\partial E}{\partial c_i}$ , and due to the multivariate chain rule, we have
$$ \frac{\partial E}{\partial w_{k,a}}
= \sum_i
\frac{\partial E}{\partial c_i}
\frac{\partial c_i}{\partial \alpha_i}
\frac{\partial \alpha_i}{\partial z_i}
\frac{\partial z_i}{\partial \phi_i}
\frac{\partial \phi_i}{\partial w_{i,u}}$$
We have
$$ \phi_{i,k} = \sum_a w_{k,a} s_{i,a}
\Longrightarrow
\frac{\partial \phi_{i,k}}{\partial w_{i,a}} = s_{i,a} $$
$$ z_{i,u} = \sum_k \phi_{i,k} \psi_{u,k}
\Longrightarrow
\frac{\partial z_{i,u}}{\partial \phi_{i,k}} = \psi_{u,k} $$
$$ \alpha_{i,u} = \frac{ z_{i,u} }{ \sum_v z_{i,v} }
\Longrightarrow
\frac{\partial \alpha_{i,v}}{\partial z_{i,u}} = \alpha_v (\delta_{u,v} - \alpha_u)
$$
$$ c_{i,b} = \sum_u \alpha_{i,u} h_{u,b}
\Longrightarrow
\frac{\partial c_{i,b}}{\partial \alpha_{i,u}} = h_{u,b}
$$
Assume that we know each $\frac{\partial E}{\partial c_{i,b}}$ , and due to the multivariate chain rule, we have
$$ \frac{\partial E}{\partial w_{k,a}}
= \sum_i
\sum_{b=1}^B
\frac{\partial E}{\partial c_{i,b}}
\sum_{v=1}^U
\frac{\partial c_{i,b}}{\partial \alpha_{i,v}}
\sum_{u=1}^U
\frac{\partial \alpha_{i,v}}{\partial z_{i,u}}
\frac{\partial z_{i,u}}{\partial \phi_{i,k}}
\frac{\partial \phi_{i,k}}{\partial w_{k,a}}$$
We introduced many $\sum$ 's in above equation. They are due to the multivariate chain rule. We need $\sum_u$ because $z_{i,u}$ is over $u$ involving all $\psi_u$ 's. We need $\sum_v$ because each $\alpha_{i,v}$ depends on all $z_{i,u}$ 's in the normalization term. We need $\sum_b$ because what we got from speller is each $\frac{\partial E}{\partial c_{i,b}}$ .
Similarly, we can compute $\frac{\partial E}{\partial U}$ as well.
We noticed that the combination of $\sum_u$ and $\sum_v$ makes a $O(U^2)$ complexity in the above equation. By using a pyramid BLSTM in the listener, we can shorten $U$ thus fasten the training.