41. 从有限状态机的角度看 parse 原理.md

从有限状态机的角度看 parse 原理

1. 有限状态机定义

有限状态机（英语：finite-state machine，缩写：FSM）又称有限状态自动机（英语：finite-state automaton，缩写：FSA），简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型。

简单的理解来说，读取一组输入然后根据输入来更改为不同的状态

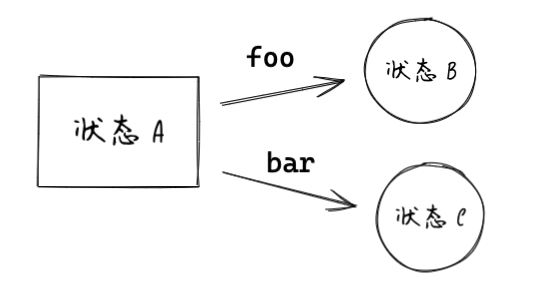
• 例如上图，给状态 A 输入 foo
• 状态 A 转向为状态 B
• 给状态 A 输入 bar
• 状态 A 转向状态 C

有限状态机经常被用在编译中。

2. parse 模块的原理

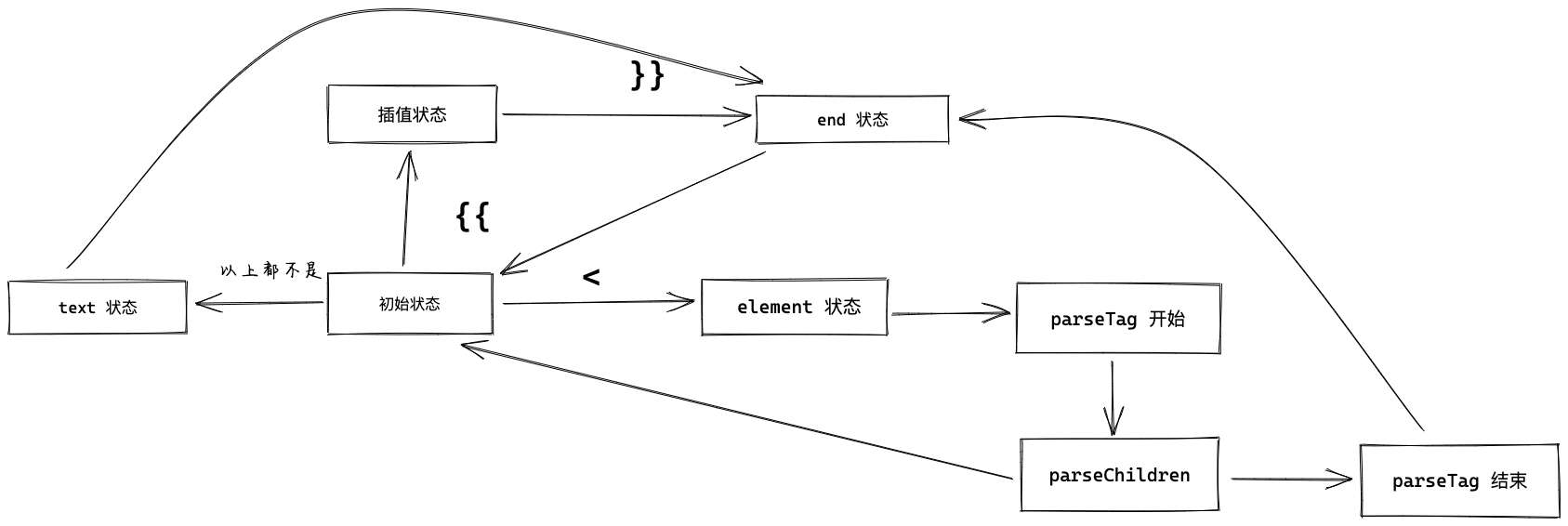
通过前几个小节中我们可以看出，其实 parse 模块也是这样的，大体会分为几个状态：

• 初始状态
• text 状态
• element 状态
• interpolation 状态
• end 状态

总结来说大概是这样的：

• 最开始是初始状态，也就是刚刚执行 createRoot，进入 parseChildren
• 如果是 {{ 开头，进入 插值状态，如果是 }} 开头，进入 end 状态，再次回到 初始状态
• 如果是 < 开头，进入 element 状态，接着会 parseTag ，parseChildren，parseTag 结束，进入 end 状态，再次回到 初始状态
• 如果以上都不是，那么进入 text 状态，进入 end 状态，再次回到 初始状态
• 每次从三种状态转为 end 状态，都会推进，最终会以 context.source 消费完毕作为出口

3. 通过有限状态机模拟正则

function test(str) {
  function stateA(char) {
    if (char === 'a') {
      return stateB
    }
    return stateA
  }
  function stateB(char) {
    if (char === 'b') {
      return stateC
    }
    return stateA
  }
  function stateC(char) {
    if (char === 'c') {
      return stateEnd
    }
    return stateA
  }
  function stateEnd() {
    return stateEnd
  }
  let currentState = stateA
  for (let i = 0; i < str.length; i++) {
    currentState = currentState(str[i])
    if (currentState === stateEnd) {
      return true
    }
  }
  return false
}

console.log(test('ac'))

• 上面的例子我们就通过有限状态机模仿了正则中的 /abc/ 的功能
• 初始状态是 stateA
• 如果输入的是 a 转为 stateB
• 如果输入的是 b 转为 stateC
• 如果输入的是 c 转为 end
• 否则都重新转为初始状态

以上就是有限状态机的基本概念，以及 parse 模块的基本原理。