Correlation Attacks of an LFSR based Stream Cipher

Description

Correlation Attacks of an LFSR based Stream Cipher in Python.

How to run the program

The program uses argparse. You need to pass a value for each following parameter:

• -S, --polynomialsize: Number of bits of the polynomial.
• -k, --keystream: Keystream in hexadecimal.
• -s, --keystreamsize: Number of bits of the keystream.
• -p, --xorposition: Positions of the bits to be xor, separated by spaces (start at 0 from the right)

For example:

python3 lfsr.py --polynomialsize <size> --keystream <keystream> --keystreamsize <size> --xorposition <pos pos ...>

Example of an attack

Consider a 64-bit combination generator with three LFSRs respectively having the following characteristic polynomials:

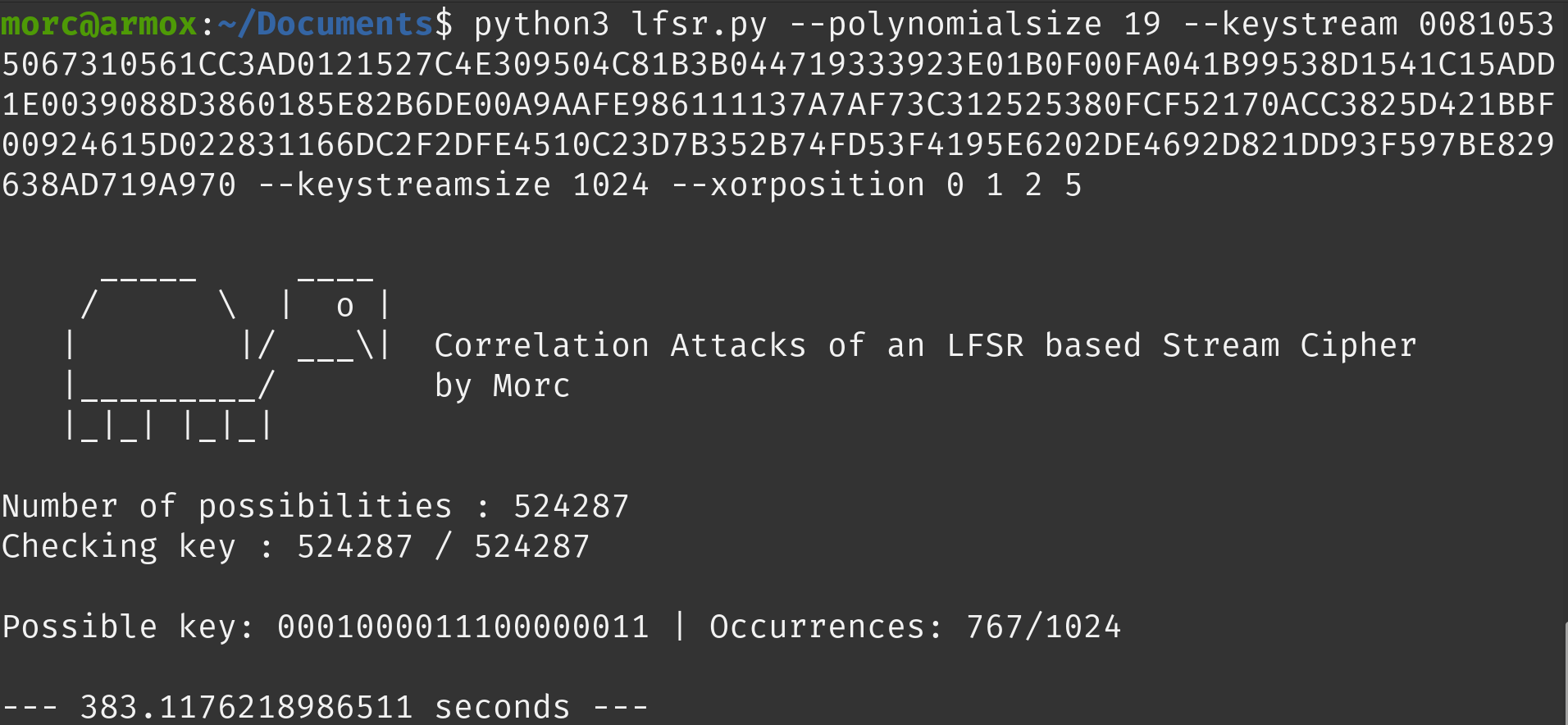
• x^19 + x^5 + x^2 + x + 1
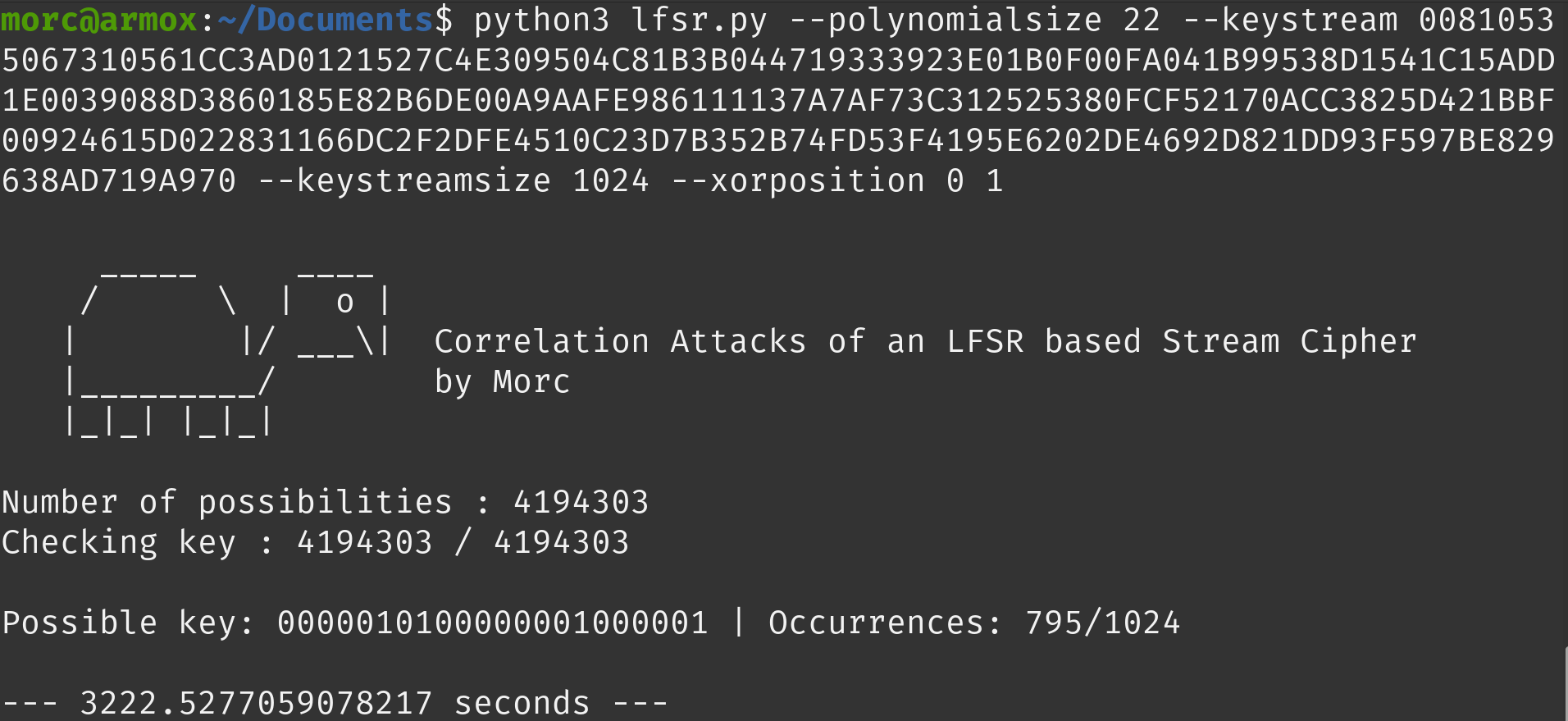
• x^22 + x + 1
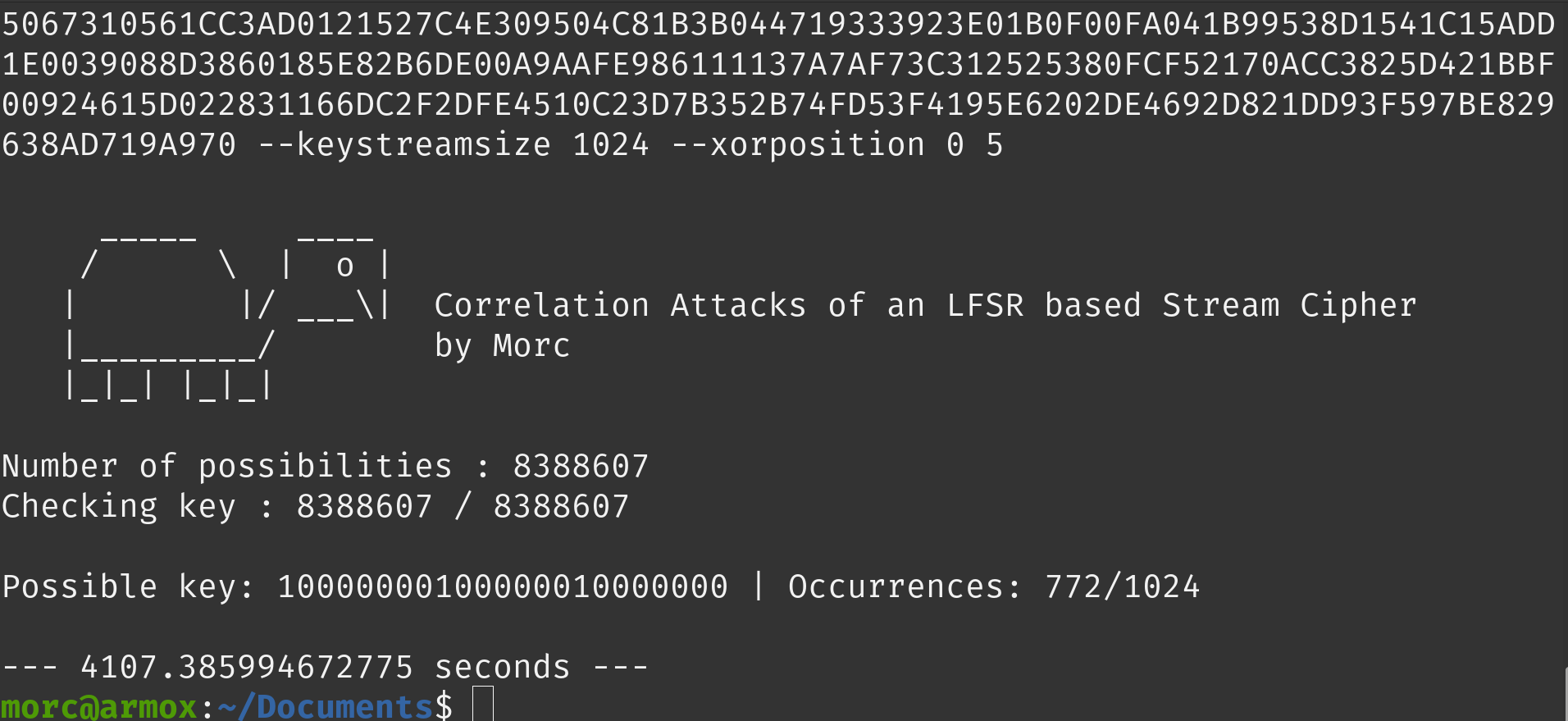
• x^23 + x^5 + 1

Suppose we have obtained the following 1024 bits of the keystream:

0x00810535067310561CC3AD0121527C4E309504C81B3B044719333923E01B0F00FA041B99538D1541C15ADD1E0039088D3860185E82B6DE00A9AAFE986111137A7AF73C312525380FCF52170ACC3825D421BBF00924615D022831166DC2F2DFE4510C23D7B352B74FD53F4195E6202DE4692D821DD93F597BE829638AD719A970

To recover the key, we need to generate the part of key with the help of the keystream and polynomials. Each polynomial generates a part of the key.

Steps of the attack

1. Calcul LFSR
   • The first step is calculating the LFSR of the polynomial to get all periods.
   • Number of periods are number of possibilities.
2. Generate bits stream for all possibilities
   • The second step is generating bits stream for each period.
   • To proceed, for each period, loop from the current period and get the last bit of each period until you have same number of bits than keystream size.
3. Compare generated bits stream with the keystream
   • For each generated bits stream, compare them with the keystream and count the number of occurrences of each same bit.
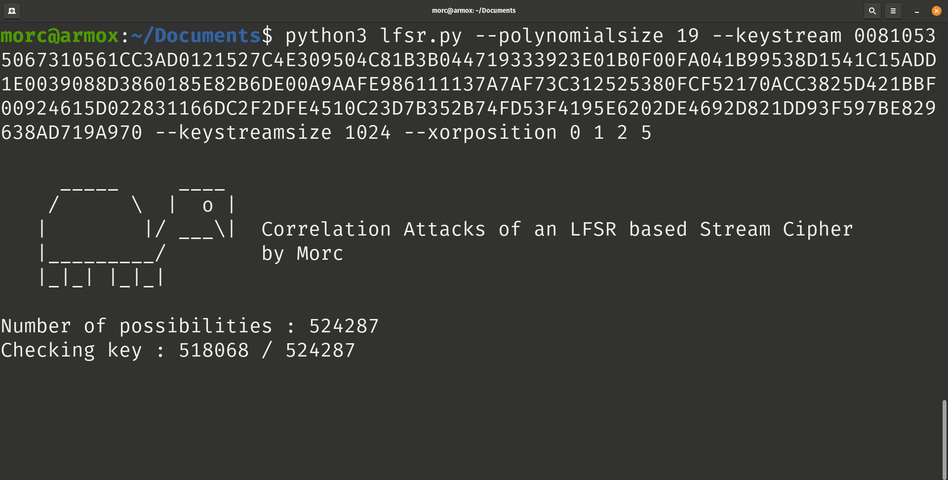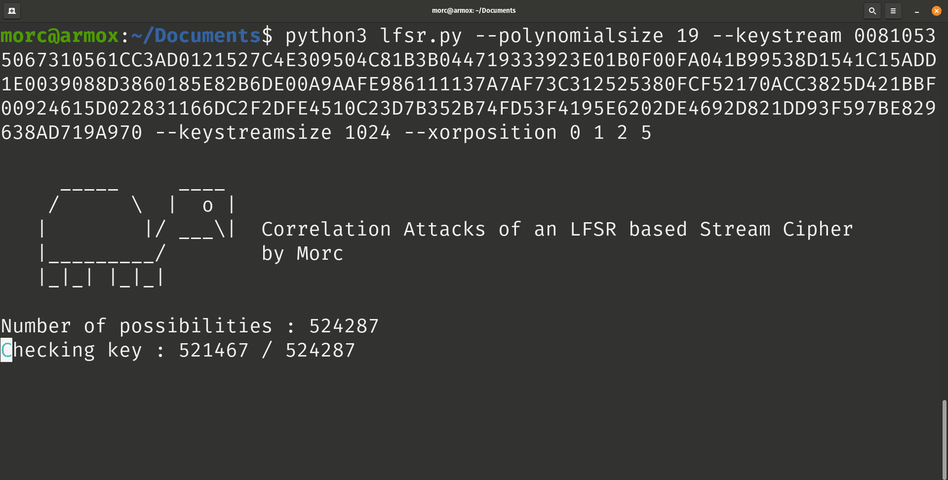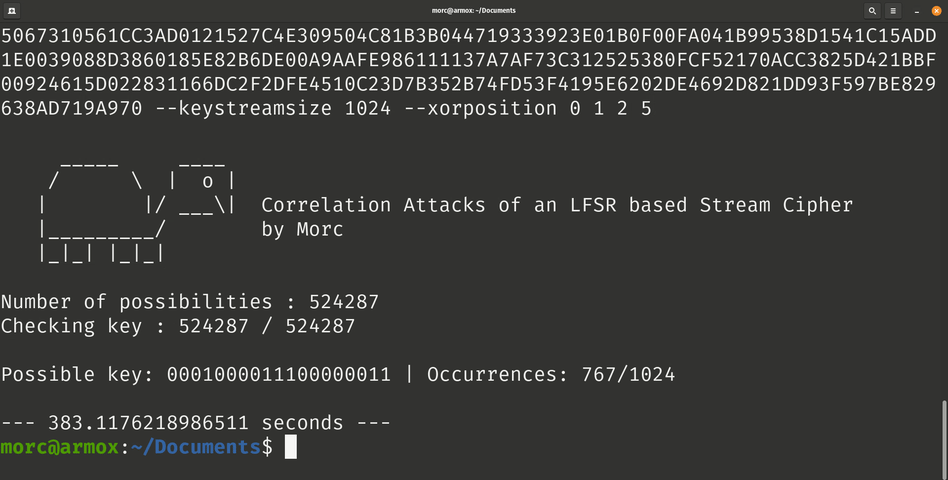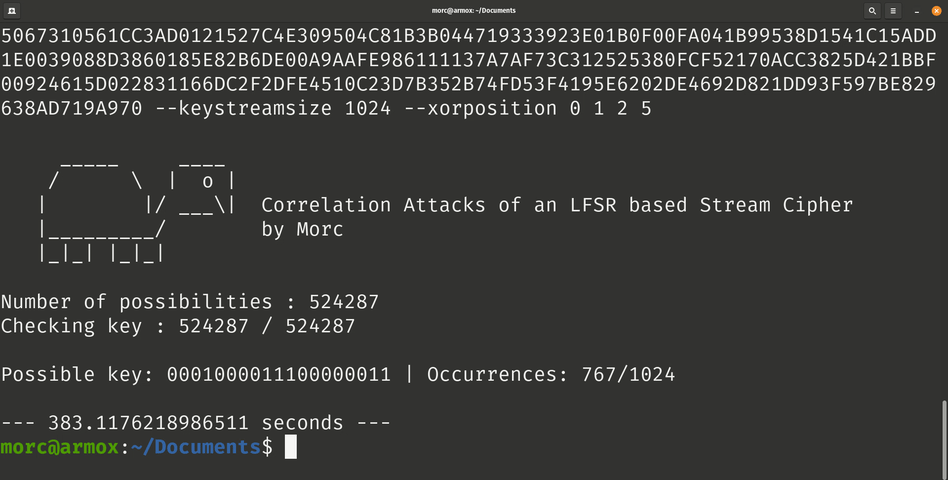
   • The generated bits stream with the best occurrences contains the possible key in the beginning (the possible key has the same number of bits than number of bits of polynomial).
4. Repeat previous steps for all polynomials
5. Recover the key
   • Put all possible key together to get the key

Result

The first polynomial is: x^19 + x^5 + x^2 + x + 1. The key found is: 0001000011100000011.

The second polynomial is: x^22 + x + 1. The key found is: 0000010100000001000001.

The third polynomial is: x^23 + x^5 + 1. The key found is: 10000000100000010000000.

The 64-bit key is: 0001000011100000011000001010000000100000110000000100000010000000 or 0x10E060A020C04080 in hexadecimal.