Basic arithmetic, integration, differentiation, evaluation, and root finding over dense univariate polynomials.
(v1.6) pkg> add PolynomialsThis package supports Julia v1.6 and later.
-
Polynomial– standard basis polynomials,$a(x) = a_0 + a_1 x + a_2 x^2 + … + a_n x^n$ for$n ≥ 0$ . -
ImmutablePolynomial– standard basis polynomials backed by a Tuple type for faster evaluation of values -
SparsePolynomial– standard basis polynomial backed by a dictionary to hold sparse high-degree polynomials -
LaurentPolynomial– Laurent polynomials,$a(x) = a_m x^m + … + a_n x^n$ for$m ≤ n$ and$m,n ∈ ℤ$ . This is backed by an offset array; for example, if$m<0$ and$n>0$ , we obtain$a(x) = a_m x^m + … + a_{-1} x^{-1} + a_0 + a_1 x + … + a_n x^n$ -
FactoredPolynomial– standard basis polynomials, storing the roots, with multiplicity, and leading coefficient of a polynomial -
ChebyshevT– Chebyshev polynomials of the first kind -
RationalFunction- a type for ratios of polynomials.
julia> using PolynomialsConstruct a polynomial from an array (a vector) of its coefficients, lowest order first.
julia> Polynomial([1,0,3,4])
Polynomial(1 + 3*x^2 + 4*x^3)Optionally, the variable of the polynomial can be specified.
julia> Polynomial([1,2,3], :s)
Polynomial(1 + 2*s + 3*s^2)Construct a polynomial from its roots.
julia> fromroots([1,2,3]) # (x-1)*(x-2)*(x-3)
Polynomial(-6 + 11*x - 6*x^2 + x^3)Evaluate the polynomial p at x.
julia> p = Polynomial([1, 0, -1]);
julia> p(0.1)
0.99Methods are added to the usual arithmetic operators so that they work on polynomials, and combinations of polynomials and scalars.
julia> p = Polynomial([1,2])
Polynomial(1 + 2*x)
julia> q = Polynomial([1, 0, -1])
Polynomial(1 - x^2)
julia> p - q
Polynomial(2*x + x^2)
julia> p = Polynomial([1,2])
Polynomial(1 + 2*x)
julia> q = Polynomial([1, 0, -1])
Polynomial(1 - x^2)
julia> 2p
Polynomial(2 + 4*x)
julia> 2+p
Polynomial(3 + 2*x)
julia> p - q
Polynomial(2*x + x^2)
julia> p * q
Polynomial(1 + 2*x - x^2 - 2*x^3)
julia> q / 2
Polynomial(0.5 - 0.5*x^2)
julia> q ÷ p # `div`, also `rem` and `divrem`
Polynomial(0.25 - 0.5*x)Most operations involving polynomials with different variables will error.
julia> p = Polynomial([1, 2, 3], :x);
julia> q = Polynomial([1, 2, 3], :s);
julia> p + q
ERROR: ArgumentError: Polynomials have different indeterminatesWhile polynomials of type Polynomial are mutable objects, operations such as
+, -, *, always create new polynomials without modifying its arguments.
The time needed for these allocations and copies of the polynomial coefficients
may be noticeable in some use cases. This is amplified when the coefficients
are for instance BigInt or BigFloat which are mutable themself.
This can be avoided by modifying existing polynomials to contain the result
of the operation using the MutableArithmetics (MA) API.
Consider for instance the following arrays of polynomials
using Polynomials
d, m, n = 30, 20, 20
p(d) = Polynomial(big.(1:d))
A = [p(d) for i in 1:m, j in 1:n]
b = [p(d) for i in 1:n]In this case, the arrays are mutable objects for which the elements are mutable
polynomials which have mutable coefficients (BigInts).
These three nested levels of mutable objects communicate with the MA
API in order to reduce allocation.
Calling A * b requires approximately 40 MiB due to 2 M allocations
as it does not exploit any mutability. Using
using MutableArithmetics
const MA = MutableArithmetics
MA.operate(*, A, b)exploits the mutability and hence only allocate approximately 70 KiB due to 4 k allocations. If the resulting vector is already allocated, e.g.,
z(d) = Polynomial([zero(BigInt) for i in 1:d])
c = [z(2d - 1) for i in 1:m]then we can exploit its mutability with
MA.mutable_operate!(MA.add_mul, c, A, b)to reduce the allocation down to 48 bytes due to 3 allocations. These remaining
allocations are due to the BigInt buffer used to store the result of
intermediate multiplications. This buffer can be preallocated with
buffer = MA.buffer_for(MA.add_mul, typeof(c), typeof(A), typeof(b))
MA.mutable_buffered_operate!(buffer, MA.add_mul, c, A, b)then the second line is allocation-free.
The MA.@rewrite macro rewrite an expression into an equivalent code that
exploit the mutability of the intermediate results.
For instance
MA.@rewrite(A1 * b1 + A2 * b2)is rewritten into
c = MA.operate!(MA.add_mul, MA.Zero(), A1, b1)
MA.operate!(MA.add_mul, c, A2, b2)which is equivalent to
c = MA.operate(*, A1, b1)
MA.mutable_operate!(MA.add_mul, c, A2, b2)Note that currently, only the Polynomial implements the API and it only
implements part of it.
Integrate the polynomial p term by term, optionally adding a constant
term k. The degree of the resulting polynomial is one higher than the
degree of p (for a nonzero polynomial).
julia> integrate(Polynomial([1, 0, -1]))
Polynomial(1.0*x - 0.3333333333333333*x^3)
julia> integrate(Polynomial([1, 0, -1]), 2)
Polynomial(2.0 + 1.0*x - 0.3333333333333333*x^3)Differentiate the polynomial p term by term. For non-zero
polynomials the degree of the resulting polynomial is one lower than
the degree of p.
julia> derivative(Polynomial([1, 3, -1]))
Polynomial(3 - 2*x)Return the roots (zeros) of p, with multiplicity. The number of
roots returned is equal to the degree of p. By design, this is not type-stable, the returned roots may be real or complex.
julia> roots(Polynomial([1, 0, -1]))
2-element Vector{Float64}:
-1.0
1.0
julia> roots(Polynomial([1, 0, 1]))
2-element Vector{ComplexF64}:
0.0 - 1.0im
0.0 + 1.0im
julia> roots(Polynomial([0, 0, 1]))
2-element Vector{Float64}:
0.0
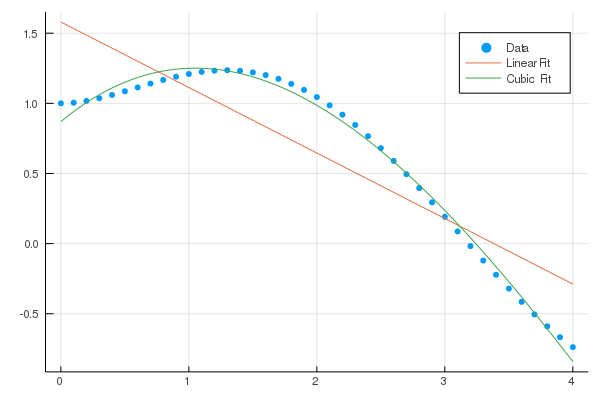
0.0Fit a polynomial (of degree deg or less) to x and y using a least-squares approximation.
julia> xs = 0:4; ys = @. exp(-xs) + sin(xs);
julia> fit(xs, ys) |> p -> round.(coeffs(p), digits=4) |> Polynomial
Polynomial(1.0 + 0.0593*x + 0.3959*x^2 - 0.2846*x^3 + 0.0387*x^4)
julia> fit(ChebyshevT, xs, ys, 2) |> p -> round.(coeffs(p), digits=4) |> ChebyshevT
ChebyshevT(0.5413⋅T_0(x) - 0.8991⋅T_1(x) - 0.4238⋅T_2(x))Visual example:
Polynomial objects also have other methods:
-
For standard basis polynomials, 0-based indexing is used to extract the coefficients of
[a0, a1, a2, ...]; for mutable polynomials, coefficients may be changed using indexing notation. -
coeffs: returns the coefficients -
degree: returns the polynomial degree,lengthis number of stored coefficients -
variable: returns the polynomial symbol as a polynomial in the underlying type -
LinearAlgebra.norm: find thep-norm of a polynomial -
conj: finds the conjugate of a polynomial over a complex field -
truncate: set to 0 all small terms in a polynomial; -
chopchops off any small leading values that may arise due to floating point operations. -
gcd: greatest common divisor of two polynomials. -
Pade: Return the Pade approximant of orderm/nfor a polynomial as aPadeobject.
-
StaticUnivariatePolynomials.jl Fixed-size univariate polynomials backed by a Tuple
-
MultiPoly.jl for sparse multivariate polynomials
-
DynamicPolynomials.jl Multivariate polynomials implementation of commutative and non-commutative variables
-
MultivariatePolynomials.jl for multivariate polynomials and moments of commutative or non-commutative variables
-
PolynomialRings.jl A library for arithmetic and algebra with multi-variable polynomials.
-
AbstractAlgebra.jl, Nemo.jl for generic polynomial rings, matrix spaces, fraction fields, residue rings, power series, Hecke.jl for algebraic number theory.
-
LaurentPolynomials.jl A package for Laurent polynomials.
-
CommutativeAlgebra.jl the start of a computer algebra system specialized to discrete calculations with support for polynomials.
-
PolynomialRoots.jl for a fast complex polynomial root finder. For larger degree problems, also FastPolynomialRoots and AMRVW. For real roots only RealPolynomialRoots.
-
SpecialPolynomials.jl A package providing various polynomial types beyond the standard basis polynomials in
Polynomials.jl. Includes interpolating polynomials, Bernstein polynomials, and classical orthogonal polynomials. -
ClassicalOrthogonalPolynomials.jl A Julia package for classical orthogonal polynomials and expansions. Includes
chebyshevt,chebyshevu,legendrep,jacobip,ultrasphericalc,hermiteh, andlaguerrel. The same repository includesFastGaussQuadrature.jl,FastTransforms.jl, and theApproxFunpackages.
As of v0.7, the internals of this package were greatly generalized and new types and method names were introduced. For compatability purposes, legacy code can be run after issuing using Polynomials.PolyCompat.
If you are interested in contributing, feel free to open an issue or pull request to get started.