Skip to content

[statistics] review of basic probability theory

Jump to bottom
Myungchul Shin edited this page Jun 28, 2018 · 47 revisions

statistics 관련된 논문이나 자료를 볼때, 항상 terminology가 이해가 안되거나 헷갈리는 부분이 있는데 여기서는 이것들을 어느정도 정리하고 가자. definition에 대해 알아보려면 이것(Probability) 혹은 이것(Linguist's Guide to Statistics)을 추천한다.

  • sample space

    • 다른 말 : 표본공간
    • set of elementary outcomes
    • 예, 주사위 던지기 시행에서라면 {1,2,...,6}

  • event

    • 다른 말 : 사건
    • subset of sample space
    • 예, {},{1},{6},{1,5},{1,4,5},....,{1,2,3,4,5,6}

  • probability measures(or simply probability)

    • 다른 말 : 확률
    • a probability measure is a function from events f : event -> [0,1]

  • conditional probability and Bayesian inversion formula

    • 다른 말 : 조건부 확률, 베이지안 공식
    • P(A | B) = P(A,B)/P(B) = {P(B | A)*P(A)} / P(B)
    • P(A) : prior probability, 아무 조건이 없는 상태에서의 확률
    • P(A | B) : posterior probability, updated probability of A knowing B, 다른 사건이 벌어진 상태에서의 확률

  • partition

    • 다른 말 : 분할
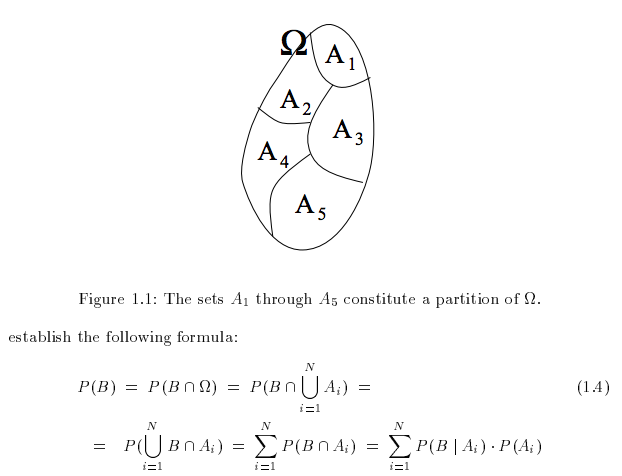
    • A(i)i=1,2,...,N가 sample space에서의 event라고 하자., A(i) != A(j)이고 'sum{P(A(i))}i=1,2,...,N = 1'을 만족할 경우, A(i)i=1,2,...,N를 sample space의 partition이라고 한다.
    • partition은 여러 응용에서 사용되는 개념인데, 대표적인 것은 아래와 같다. partition

  • random variable

    • 다른 말 : stochastic variable, 확률변수 -> support, probability function의 x축
    • function from sample space to real numbers
      f : elementary event -> R
    • 직관적으로 생각하면 sample space를 어떤 실수로 매핑시켜둔것인데, 예를 들면 주사위던지기에서
      f : {one,two,three,four,five,six} -> {1,2,3,4,5,6}

  • discrete and continuous random variable

    • 다른 말 : 이산확률변수, 연속확률변수
    • discrete : random variable is finite or countable
      • 예) X = {1,2,3,4,5,6}
    • continuous : random variable is continuous and differentiable except a finite number of points
      • 예) X = [-infinite,+infinite]

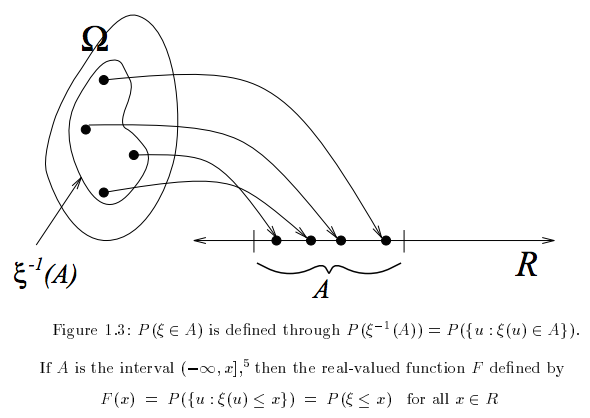
  • distribution function(of a random variable)

    • 다른 말 : cumulative distribution function(cdf)
    • random variable X가 어떤 x보다 작거나 같은 경우, [-infinite,x], 이것의 확률값
    • 보통 F(x)라고 표현한다. distribution_function

  • probability function(of a random variable)

    • 다른 말 : frequency function, f(x), probability distribution function, probability distribution
    • for discrete random variable X : f(x) = P(X=x)
      • probability mass function(pmf), 확률질량함수
    • for continuous random variable X : f(x) = F'(x) = d[F(x)]/dx
      • probability density function(pdf), 확률밀도함수

  • expectation(of a random variable)

    • 다른 말 : 기대값, statistical mean of random variable(stochastic variable), mean
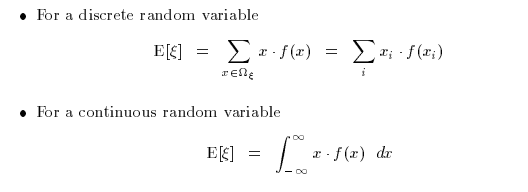
      expectation
    • X ~ f(X)에서 E(X)는 결국 random variable X의 확률적 무게중심이라고 볼수도 있다. 어쨌든 x축에 존재

  • variance

    • 다른 말 : 분산
    • mean과 차이의 제곱에 대한 expectation으로 정의한다. variance
    • variance는 standard deviation(표준편차)의 제곱이다.

  • Bernoulli distribution

    • 다른 말 : 베르누이 분포
    • 예) 동전던지기를 1번 시행했을 때, 앞면/뒷면이 나올 확률
    • sample space = {F,S}
    • random variable = X = {0,1}
    • probability distribution of random variable X and parameter p = P(X=1)
    • f(x) = px(1-p)1-x for x={0,1}
    • E(X) = p
    • a sample drawn from pmf f(x)
      • sample = { 0,1,1,0,1,0,0,....,1 }, size = n

  • binomial distribution

    • 다른 말 : 이항분포
    • 예) 동전던지기를 n번 시행하고 앞면이 k번 나온 경우에 대한 확률
    • Bernoulli 시행을 n번 수행하면 sequence가 나온다.
      • 예) 'SSFFFSSFSFFSSS....'
      • basic sample space = {S,F}
      • sample space = {S,F} X {S,F} X ... X {S,F} (n factors)
      • sample space -> map -> random variable X = {0,1,...,n} (number of success)
      • P(X=k) = nCk * pk(1-p)n-k
        nPk = n*(n-1)...(n-k+1) = n!/(n-k)!, nCk = nPk / k!
      • E(X) = np, Var(X) = np(1-p)
        binomial distribution plot
    • sample space의 elementary event에 대해서 헷갈리는 부분
      • 예) '11000','10100','10010',... 이와 같이 1이 2번 나오는 elementary event들은 전부 X=2로 매핑된다.
      • Q: P('11000') = p2(1-p)3 (?)
      • A: '11000'에서 1이 있는 위치는 순서에 무관하다고 정의했으므로 '11000','10100','10010'은 전부 같은 event이다.
        • 따라서, P('11000') = 5C2 * p2(1-p)3 = P('10100') = P('10010') = ...
    • a sample drawn from pmf P(X=k;p)
      • sample = {'110011...','10001101...','0001010...',...}, size = m
    • n=1일때는 Bernoulli distribution

  • categorical distribution

    • 다른 말 : 카테고리 분포, generalized Bernoulli distribution
    • 베르누이 분포를 일반화한 개념.
      • sample space = {1,...,k}, k possible outcomes
      • random variable X = {1,...,k}
      • P(X=i) = pi for i = 1,..,k
        • sum{P(X=i)}i=1,..,k = 1
      • P(X=i)는 다른 방식으로도 표현 가능하다.
      • E(X) = P
        • P = [p1,p2,...,pk]
        • categorical distribution의 기대값은 Bernoulli와는 다른게 k-dimensional vector로 표현
    • k=3일때 2-simplex
      simplex
    • 1-simplex는 Bernoulli distribution의 확률 p+q=1에 대해서 그려볼 수 있다.
    • a sample drawn from pmf P(X=i)
      • sample = {1,3,2,4,1,5,3,1,4,4,5,....}, k=5, size = n

  • multinomial distribution

    • 다른 말 : 다항분포, generalization of binomial distribution, 'one of the most important multivariate distribution'
    • 이항분포를 일반화한 개념
    • 예) 주사위던지기를 60번 수행했을 때, 각 눈금이 X=[8,12,5,15,14,6] 이렇게 나올 확률
    • binomial distribution은 기본적으로 Bernoulli trial을 n번 수행한 결과가 sample space가 되는데, 비슷하게 multinomial distribution에서는 categorical distribution을 따르는 trial을 n번 수행한 결과가 sample space가 된다.
    • k-way categorical distribution에서 P(X=i)=pi(i=1,...,k)
      sequence = '1215444433335....k....1...'
      여기서 각각의 i에 대한 발생 횟수를 x(i)라고 하면
      X = [x(1),x(2),x(3),...,x(k)], x(i) = {0,1,2,...,n}, sum{x(i)} = n for i=1,..,k random vector X는 multinomial distribution을 따른다고 말한다.
      multinomial_distribution
    • 위 수식에서 경우의 수가 어째서 그렇게 나오는가?
      • 기본 개념은 n개에서 x(1)개를 선택하는 경우의 수는 nCx(1), 이렇게 선택한 이후에 남아있는 칸은 'n-x(1)'
      • 다시 'n-x(1)'에서 x(2)개를 선택하는 경우의 수는 n-x(1)Cx(2)
      • 이런식으로 해서 모든 경우의 수를 곱하면 된다.
    • multinomial distribution은 gamma function을 사용해서 아래와 같이 표현 가능하다.
      multinomial_distribution_gamma
    • a sample drawn from pmf f(x(1),x(2),...,x(k); n; p(1),p(2),...,p(k))
      • sample = {'11223...','23432...','554324...',...}, size=m
    • n=1 일때 categorical distribution

  • normal distribution

    • 다른 말 : 정규분포, Gaussian distribution
      normal distribution
    • 예) 대부분의 자연현상, 대한민국 인구 나이 분포, 학생들의 키 분포, ...
Clone this wiki locally