C++ implementation of the famous percolation problem. In particular, this problem is presented in Coursera's "Algorithm" course as a good candidate for applying the Union-Find algorithms.
Even though the course makes extensive use of Java, this wants to be an alternative implementation in C++.
The problem is described in great detail here, the following is just a summary.
Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations.
We model a percolation system using an n-by-n grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)
| System that percolates | System that does not percolate |
|---|---|
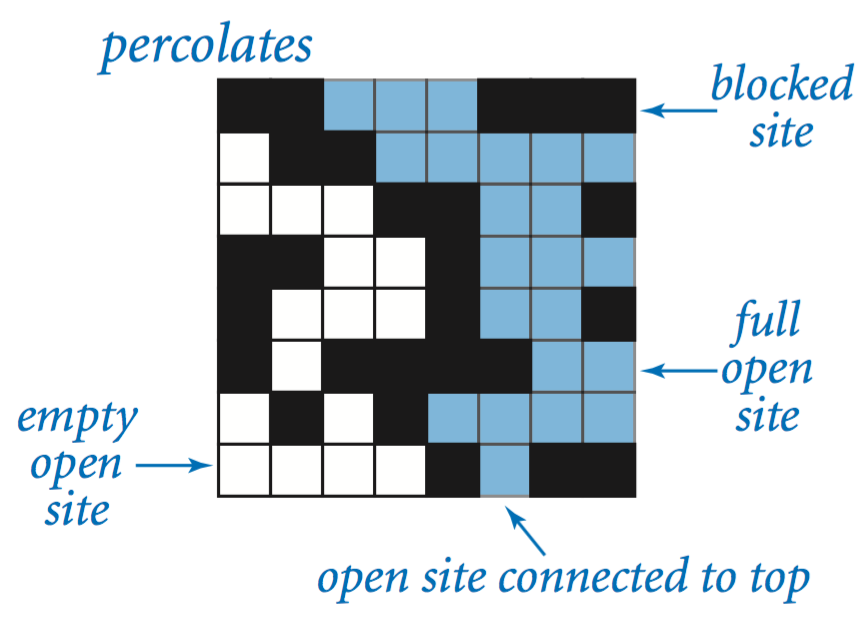 |
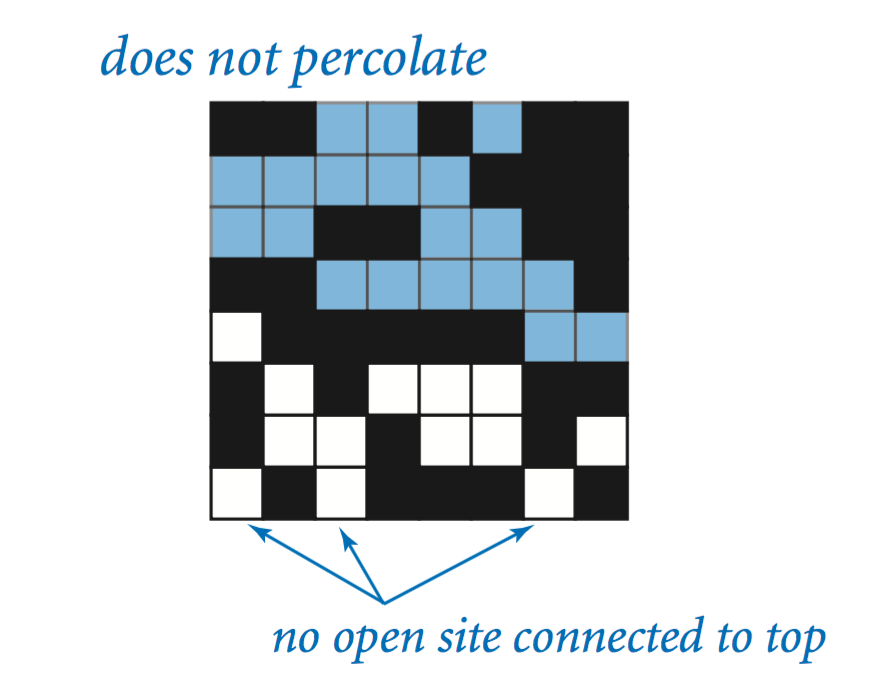 |
In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1 − p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. When n is sufficiently large, there is a threshold value p* such that when p < p* a random n-by-n grid almost never percolates, and when p > p*, a random n-by-n grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived.
Clone the repo with
git clone https://github.com/giacomo-b/percolation.git
or, as an alternative, download as a .zip file.
Navigate to the repo folder and issue
make
or make all. If you wish to use another compiler you can either edit the Makefile or import the files into you favorite IDE.
If no input is provided, 50 experiments are performed on 1000 x 1000 matrices. In alternative you can specify two inputs which represent the number of elements per side and the number of trials. For example, to run 100 experiments on 2000 x 2000 matrices, do the following:
./main 100 2000
PercolationStats runs Monte Carlo simulation by:
- Initializing a n-by-n grid with all sites completely blocked
- Iterating the following until the system percolates
- Choose a site uniformly at random.
- If the site is not open, open it.
- Computing the fraction of open sites to get an estimation of the percolation threshold
It repeats the above trials times in order to compute the final statistics, namely: mean, standard deviation, 95% confidence interval.
In addition:
Percolationis the actual percolation class that keeps track of open sites, input site validation, checks if the sites are open, etc.Timer.his a header used to get the execution time of a particular scope (makes use of RAII). To use, just writeTimer name_of_timer;and it will automatically destroy at the end of the scope where it has been declared.WeightedQuickUnionimplements the weighted quick union union-find algorithm to balance trees during a normal quick union execution.
- Accept user input
- Parallelize Percolation objects instantiation and percolation computations