-
遞迴定義 : 節點比左子樹都大,比右子樹都小
-
高度決定搜尋效率
-
不適合用已排序的資料,退化成linked list,複雜度為O(n)
-
和紅黑樹同是二元搜尋樹,搜尋值的方式也一樣( >Value 往右找,< Value 往左找 )
-
Traversal (和紅黑樹同)
- Inorder (left->root->right)(較常用)
- Preorder (root->left->right)
- Postorder(left->right->root)
Ex:
4
/ \
2 6
/ \ / \
1 3 5 7
* Preorder : 4 213 657
* Inorder : 123 4 567
* Postorder : 132 576 4
- FindMin : 沿著左子樹走到底
- FindMax : 沿著右子樹走到底
- FindPredecessor : 小於當前節點的最大值
- FindSuccssor : 大於當前節點的最小值
- Delete : 找前驅節點或後繼節點來替代
- 葉節點直接刪除
- 只有一個子節點直接拿來替代 (本質上就是找前驅或後繼節點)
- 有兩個子節點的,需要找到替代節點 (前驅或後繼節點,都可以)
- 和紅黑樹相同,只是因為刪除可能會破壞紅黑數的平衡,所以多了著色、旋轉過程
- BST 缺點 : 退化問題 (solve AVL Tree)
- 具所有 BST 的特性
- 兩種最具代表的自平衡樹
- AVL Tree
- RB Tree
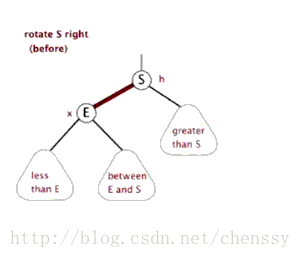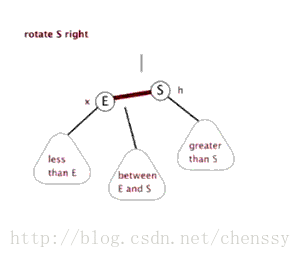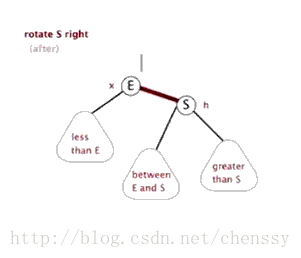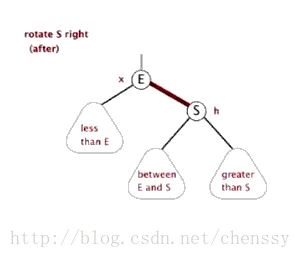
精神: 樹的高度不超過 1 (旋轉後續會仔細提到)
Ex : insert 10, 9, 8, 7, 6, 5 ,4, 3, 2, 1,共六次旋轉
insert 8 (10不平衡)
10 9
/ / \
9 ----------> 8 10
/ (R-rotate)
8
insert 7
9
/ \
8 10
/
7
insert 6 (8, 9 不平衡)
9 9
/ \ / \
8 10 7 10
/ ----------------> / \
7 (R-rotate to 8) 6 8
/
6
insert 5 (9 不平衡)
9 7
/ \ / \
7 10 ----------------> 6 9
/ \ (R-rotate to 9) / / \
6 9 5 8 10
/
5
insert 4 (6 不平衡)
7 7
/ \ / \
6 9 ----------------> 5 9
/ / \ (R-rotate to 6) / \ / \
5 8 10 4 6 8 10
/
4
insert 3
7
/ \
5 9
/ \ / \
4 6 8 10
/
3
insert 2 (4, 5 不平衡)
7 7
/ \ / \
5 9 5 9
/ \ / \ / \ / \
4 6 8 10 ----------------> 3 6 8 10
/ (R-rotate to 4) / \
3 2 4
/
2
insert 1 (5 不平衡)
7 7
/ \ / \
5 9 3 9
/ \ / \ / \ / \
3 6 8 10 ----------------> 2 5 8 10
/ \ (R-rotate to 5) / / \
2 4 1 4 6
/
1
-
黑色節點平衡(每條path的黑色節點數量相同),但是有可能不是AVL樹 以下圖為例,是紅黑樹但不是AVL樹,所以紅黑樹的性質是介於BST和AVL之間的,AVL Tree 相對來說條件太嚴格了😅😅
-
AVL 樹實現較複雜,且插入跟刪除性能較紅黑樹差,實際應用紅黑樹較廣泛
-
Ex : Java HashMap, TreeSet,Java 8 因為把 Hashmap 用紅黑樹取代Linked list,性能提升不少
-
來自 2-3-4 樹
-
所有葉節點有相同深度
-
節點只能有 2-節點, 3-節點, 4-節點
- 2-節點 : 包含 1 個元素的節點,有 2 個子節點
- 3-節點 : 包含 2 個元素的節點,有 3 個子節點
- 4-節點 : 包含 3 個元素的節點,有 4 個子節點
-
所有節點至少有一個元素
-
一定要是 Full complete tree (葉子全滿,且存在)
-
RB tree 的起源,查詢如普通的BST,但是節點元素個數不確定,可能需要其他資料結構儲存或表示,所以不易實現。
-
位置滿了讓中間的數字升一層,如同B-Tree之類的多路查詢樹
-
紅黑數新增的一定是紅色的
-
2-3-4 Tree 可轉成多個紅黑樹,但一個紅黑樹只能轉成一種 2-3-4 Tree
-
2-節點 : 黑色
-
3-節點 : 上黑下紅 (左頃或右頃) --> 可以有兩種型態,造就對應多種紅黑樹的情形
-
4-節點 : 紅黑紅 (上黑下紅,中間黑且下面兩個紅)
-
裂變 : 看圖例 (如果裂變是根節點,則再次轉為黑色,中間升層變紅色,下面兩個變黑色,進來的紅色看值靠近)
Ex: 原 2-3-4 樹
可以觀察出
- 每條從根走到葉的的路徑黑節點樹相同
- 紅色節點不會單獨存在,一定和紅節點上面的黑色節點是一個整體
紅黑樹 + 新增節點(紅色) = 對等 2-3-4 樹新增一個節點
- 節點是紅或是黑
- 根是黑色
- 所有葉子都是黑色(葉子是NULL節點)
- 每個紅色節點必須有兩個黑色子節點,且根到葉子的路徑上不可以有兩個連續的紅色節點
- 任一個節點到每個葉子的所有簡單路徑都包含相同數目的黑色節點 (黑色平衡)
-
節點是紅或是黑 ===> 甭推
-
根是黑色
-
所有葉子都是黑色(葉子是NULL節點) ===> 甭推
-
不可以有兩個連續的紅色節點
-
任一個節點到每個葉子的所有簡單路徑都包含相同數目的黑色節點 (黑色平衡)
- 2-3-4 樹葉子高度都相等(Full Complete Tree),且每個節點轉乘紅黑樹後必有一個黑色,所以即可得此性質,簡單吧
一般二元搜尋樹的刪除

刪除方案 :
-
刪除葉子節點,直接刪除
-
刪除的節點有一個子節點,用子節點覆蓋
-
如果刪除的節點有兩個子節點,要找到前驅或後繼節點
- 找到前驅節點,複製前驅節點的值直接覆蓋到準備被刪除的節點的值,然後刪除前驅節點
- 找到後繼節點,複製後繼節點的值直接覆蓋到準備被刪除的節點的值,然後刪除後繼節點
- 被刪除的前驅或後繼只有兩種情況
- 被刪節點是葉子節點
- 被刪節點只有一個子節點
對等關係
- 注意,因為紅黑樹是由 2-3-4樹 轉換的,2-3-4樹每個節點至少都是 2 節點,所以左右節點一定存在,和二分搜尋樹不同
- 紅黑樹倒數兩層為 2-3-4 樹的葉子節點
- 紅黑樹上面的刪除節點一定是2-3-4樹上面的葉子節點,因為如上一小段所述,刪除節點由前驅或後繼節點替代,而前驅、後繼正好就是紅黑數或是2-3-4樹的葉子節點
- 自己能搞定(最簡單) : 2-3-4 樹 3,4 節點刪除一個節點合法 對應葉子節點是3節點或是 4 節點 所以紅色節點刪掉不用調整
- 自己不能搞定(沒小孩) : Ex: 刪除 5 or 3,刪了就非法。要跟兄弟借,但是兄弟不借,父親下來幫忙,兄弟找一人去替代父親
找真正兄弟

四節點的情形:
-
第一種情況 : 2-3-4借一個節點,紅黑樹要旋轉兩次
-
第二種情況 : 2-3-4兩個節點,紅黑樹要旋轉一次
-
找兄弟借,兄弟沒得借(情同手足,再自損)