fitness_landscape_timing

library(tree)

p <- ebt_base_parameters()

p$add_strategy(new(Strategy, list(lma=0.0648406)))

p$add_strategy(new(Strategy, list(lma=0.1977910)))

p$seed_rain <- c(1.1, 1.1)               # Starting rain.

Work out what the equilibrium seed rain is. This takes a while! If using the second set of seed_rain values this should converge quickly once the cohort schedule is worked out.

res <- equilibrium_seed_rain(p)

## 1: Splitting {9,23} times (141,141)
## 2: Splitting {1,3} times (150,164)
## *** 1: {1.1,1.1} -> {7.738,29.13} (delta = {6.638,28.03})
## 1: Splitting {15,25} times (141,141)
## 2: Splitting {4,28} times (156,166)
## 3: Splitting {1,12} times (160,194)
## 4: Splitting {0,6} times (161,206)
## *** 2: {7.738,29.13} -> {7.976,23.42} (delta = {0.2382,-5.71})
## *** 3: {7.976,23.42} -> {8,23.24} (delta = {0.02382,-0.1779})
## *** 4: {8,23.24} -> {8.001,23.23} (delta = {0.0008665,-0.01203})
## *** 5: {8.001,23.23} -> {8.001,23.23} (delta = {6.738e-05,-0.0004422})
## *** 6: {8.001,23.23} -> {8.001,23.23} (delta = {1.955e-06,-3.372e-05})
## *** 7: {8.001,23.23} -> {8.001,23.23} (delta = {1.191e-07,-1.521e-06})
## Reached target accuracy (delta 1.52064e-06 < 1.00000e-05 eps)

Set the seed rain back into the parameters

p$seed_rain <- res$seed_rain[,"out"]

schedule <- res$schedule

Resident lma values:

lma_res <- sapply(seq_len(p$size), function(i) p[[i]]$parameters$lma)

OK, good to reasonable accuracy; the seed rain values should be close enough to 1.

cmp <- fitness_landscape("lma", lma_res, p, schedule)

cmp # This should be about zero, plus or minus 1e-5 or so.

## [1] -2.467e-06 -1.668e-03

# Mutant LMA values, in increasing numbers, to test how the time

# requirements scale with the number of strategies.  Should be

# sublinear.

seq_log <- function(from, to, length.out) {
  exp(seq(log(from), log(to), length.out=length.out))
}

lma_2  <- seq_log(0.03, 0.8, 2)

lma_4  <- seq_log(0.03, 0.8, 4)

lma_8  <- seq_log(0.03, 0.8, 8)

lma_16 <- seq_log(0.03, 0.8, 16)

lma_32 <- seq_log(0.03, 0.8, 32)

lma_64 <- seq_log(0.03, 0.8, 64)

(t_2  <- system.time(w_2  <- fitness_landscape("lma", lma_2,  p, schedule)))

##    user  system elapsed 
##  17.196   0.033  17.310

(t_4  <- system.time(w_4  <- fitness_landscape("lma", lma_4,  p, schedule)))

##    user  system elapsed 
##  25.369   0.052  25.545

(t_8  <- system.time(w_8  <- fitness_landscape("lma", lma_8,  p, schedule)))

##    user  system elapsed 
##  40.851   0.078  41.111

(t_16 <- system.time(w_16 <- fitness_landscape("lma", lma_16, p, schedule)))

##    user  system elapsed 
##  75.004   0.198  76.102

(t_32 <- system.time(w_32 <- fitness_landscape("lma", lma_32, p, schedule)))

##    user  system elapsed 
## 161.520   0.434 164.307

(t_64 <- system.time(w_64 <- fitness_landscape("lma", lma_64, p, schedule)))

##    user  system elapsed 
## 311.256   0.874 317.624

tt <- c(t_2[["elapsed"]],
        t_4[["elapsed"]],
        t_8[["elapsed"]],
        t_16[["elapsed"]],
        t_32[["elapsed"]],
        t_64[["elapsed"]])

n <- 2^seq_along(tt)

This is largely OK, but the increased per-mutant time is concerning (might be due to running other things at the same time though)

plot(n, tt / n, log="x")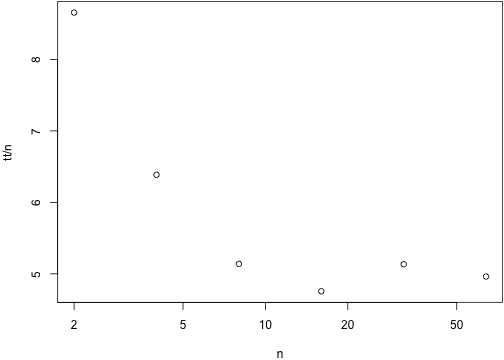

plot(w_64 ~ lma_64, type="l", log="x")

abline(v=lma_res, lty=3, col="grey")

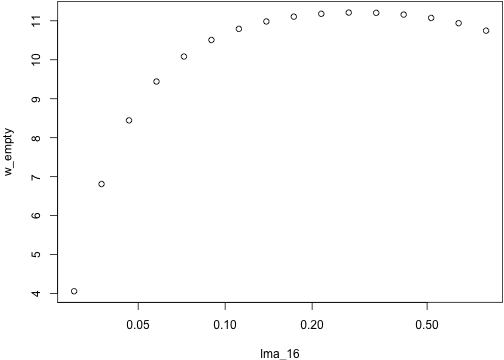
# Fitness of the mutants in an empty landscape:

w_empty <- fitness_landscape_empty("lma", lma_16, p, schedule)

plot(w_empty ~ lma_16, log="x")