-
Notifications
You must be signed in to change notification settings - Fork 27
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
EMA for BCH (part 2) #62
Comments
|
I've added ASERT to my fork of the kyuupichan http://ml.toom.im:8051/ Also, here's Mark Lundeberg's paper about ASERT: |
|
Edit/Note: The data presented in this comment are obsolete, due to incorrect window size settings. Accurate data can be found in this comment instead. Here's some more data from an unpublished version of my sim. I added a proper LWMA. I notice that it takes a 240-block half-window LWMA (480-tap filter) to have the same responsiveness as ASERT-144 or WTEMA-144. ASERT and WTEMA perform identically, so I didn't include both at all N values. CW-144 is awful, as expected -- steady-hashrate miners earn 13% less by mining BCH instead of BTC. WT-144 and WT-190 (or WHR as you call it?) are mediocre in this test. I'm curious why it performs worse in my testing than in yours. Everything else is pretty competitive, with the EMAs and LWMA at 288 blocks performing slightly better than other window sizes. Profitability of different mining strategies
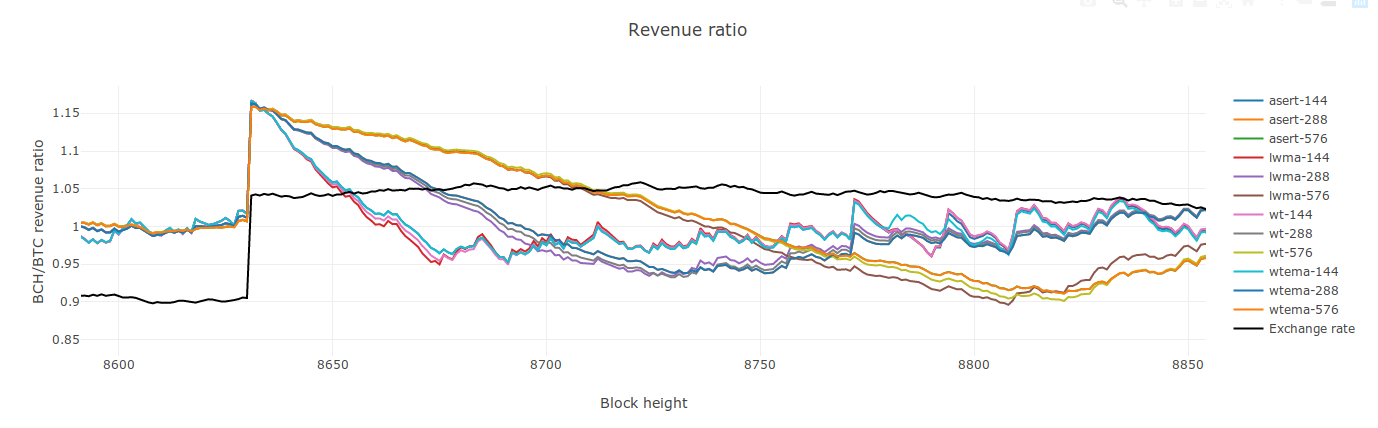
The WT algos have weird glitchy excursions, like at blocks 7365 and 7422, which are completely absent from the other algorithms. Parameters: 20k blocks, 300 PH/s steady HR, 10 EH/s variable, 1 EH/s greedy. Greedy threshold 3%. |
|
Three quick comments:
|
|
I did not realize the numbers in wtema-144 and asert-144 were "half lives" instead of the actual tau/T and alpha_recip inputs. To compare the DA's fairly, do runs like this: Once you decide a winner after testing for this particular N, that DA will very likely always be your winner for any consistent change to N which means it will always be your winner. My LWMA and ASERT runs above show it's very difficult to see any difference between them which indicates this "matching Std Devs" method is good. The WT glitch you see should go away once you give it this higher N. I just checked my WT (WHR) code and your WT code and they should be the same. The Weighted Harmonic in these names refers to the calculation on the D/st values which is mathematically the same as Tom's target * time code. LWMA is avg(D) / weighted_mean(st) so I dropped the "WH".
Mark's tweet solves the hard step in implementing an integer based e^x, although it may take a little work to figure out how to use what he said in a complete e^x. But as we know, for large N, wtema will be the same. |
|
Once you settle on a given set of assumptions that lead to a given set of tests, then you can apply the tests to all the algos. You have to also have a metric for success. Mine is that the winning DA is the one with the least % stolen plus % delays under all on-off settings of different sizes of HR "attacks" and different starting / ending percentages of a baseline D. You make an initial guess for N as I define it above. After your tests indicate a winner for that N, you use that DA for different N's. Once you find an optimum N for that DA, there should be no other DA for any other N that will give a better result. This is if you do not change your tests and metric and if my theorizing and your testing are both correct (or equally wrong). But my charts above show LWMA, EMA, and ASERT for N>30 are basically the same thing. WT is detectably a little different. BTW, Digishield's N in terms of SMA / LWMA needs to be N/4 due to it "diluting" the timespan by 4. The Std Dev confirms this. For SMA N=144, this is Digishield N=36 instead of N=17. Here's the same conditions above to compare ASERT and Digi N=36. "Improved" means the ~6 block MTP delay has been removed to help Digishield perform better. Default Digishield would have been 2x worse for BCH than CW-144. Digishield is an "SMA inside of an EMA" with N=4. |
|
I'm not too worried about the floating point issue. It's a mild annoyance to construct a MacLaurin or Taylor series for e^x or 2^x, but it's definitely doable. @jacob-eliosoff I used float math in my initial python asert implementation out of laziness and the desire to get the algo working quickly, not because I intend that to be how it would finally be implemented in C++. I'll fix it soon-ish. As I see it, the wtema vs asert debate centers on the following issues:
Any other considerations that I'm missing?
Ah, yes, I see the issue. The WT code was treating N as the window size, whereas the LWMA and EMA code was treating N as the half-life or half-window size. Will fix. |
|
With fixed N for wt, and sorted by N, and with bold for the winner at any given N: Profitability of different mining strategies
Edit: fixed N values a second time Edit2: I'm going to change this again |
|
asert-144: These tests results are from code that isn't on my repo yet.
The most recent data includes that. Edit: I'm changing most of these in a second. |
|
N = alpha_recip = tau/block_time = 144/ln(2) = 208 |
|
@jtoomim, definitely not criticizing your implementation, but it is strongly preferable that the algo fundamentally not depend on floating-point. Yes there are integer-math approximations, but they add computation steps and, above all, complexity (in the plain English sense), leading to 1. greater risk of bugs/exploitable cases and 2. bikeshedding - there are many possible approximations. The |
|
Okay, new settings for N etc: These settings result in the step response for all four algorithms clustering closely for each responsiveness setting:
This seems wrong. Including the extra 32% (190/144) seems to mess it up. If I use that 32% factor, WT ends up as a clear outlier on the impulse response. I've removed it. |
|
@jtoomim looking good! Apples-to-apples. |
|
I suspect this is immaterial but 576 maps more closely to 831 than 832: 576 / ln(2) = 830.99. For testing purposes you could even maybe pass in floating-point windows just to make sure these diffs aren't distorting the comparisons, dunno... |
|
Also to be very clear, the algo of Tom's I've been praising since I saw it is |
Confirmation times
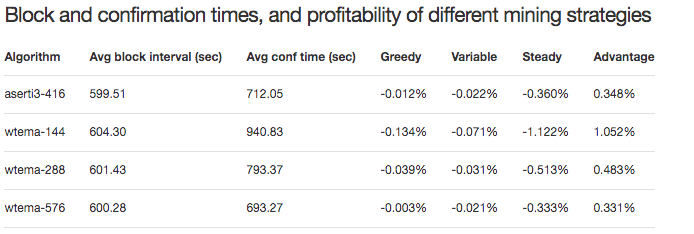
The confirmation time is the expected amount of time needed to confirm a transaction issued at a random time. This is greater than the average block interval because a random instant is more likely to be in a long block interval than a short one. Profitability of different mining strategies
cw-144/2 is a 144-block window, equivalent in impulse response to lwma-072. |
|
@jacob-eliosoff wt-144 was performing poorly until I changed the window size from 144 blocks to 288 blocks. That is, I made "144" the half-window size, just like it is for LWMA and half-life for EMA. With this change, it performs about as well as LWMA and EMA. I'm not seriously considering it as the next BCH DAA. I've mostly only been including it in the analysis because zawy12's analysis showed it to be much better than my initial analysis did, which was a discrepancy that was worth investigating and fixing. I agree: floating point math is bad. However, the main cost of wtema's use of addition instead of exponentiation is that wtema has a singularity when I'll take a closer look at your |
|
Notice asert can't be seen because it's always exactly under wtema, except a little after block The "equivalent std dev" numbers I gave are barely to 2 significant figures and since the only difference above is mostly in the in the 3rd significant figure, it's still hard to determine if any is better than the others. It's a mystery that your lwma and wt need the same N. I have two completely different programs that show N_wt = 190/144 * N_lwma gives the same std dev (constant HR) and look nearly identical to step responses like this: |
|
@jtoomim, your comments on I didn't spend a lot of time on the integer math hacks in
Hmmm. It seems to me that with stable hashrate, the expected confirmation time should be exactly 10 minutes. (You're more likely to start waiting during a long block than a short one; but you also start on average halfway through the block rather than at its beginning, and these two factors are supposed to exactly balance out.) Maybe what this reflects is that when hashrate and thus difficulty adjusts, block times get more likely to be very long (also very short but that's irrelevant), which bumps up confirmation times for the reason you described? So, the more hashrate shenanigans, the higher the expected conf time? |
Yes, that's correct. If I get rid of the switch miners, confirmation times get very close to 600 seconds (+/- 1.2%) for all algorithms. I'm using confirmation time as a summary metric of how much the block intervals deviate from an ideal Poisson process. |
That's probably just the greedy hashrate switching off slightly earlier for wtema-144 than for the other algorithms. Prior to that jump, wtema-144 was ever so slightly lower than lwma-144 and asert-144, which means the revenue ratio could have fallen below the 1.03 threshold for the 1 EH/s of greedy hashrate one block earlier. That, in turn, could have resulted in one or two unusually long block intervals, triggering the following jump in profitability. |
|
Your metric implies the larger the N, the better. There must be some counter-force to that. There needs to be a metric that balances the need for stability (high N) with the need to respond quickly to BTC/BCH price variation (low N). My intuitive assumption has been that we want to set N so that accidental variation is equal to the expected price variation (both in % per day). If we want accidental variation to be 1/2 of price variation, then we would need N to be 4x larger which would make it 4x slower to respond to price changes. |
No, it implies that the optimum N is near or above the high end of the range that was tested. Confirmation times
Profitability of different mining strategies
|
|
@jacob-eliosoff I stressed in the livestream the importance of not confounding a blocktime with any prior difficulty other than the one at which that block was mined. The original BTC algo, wtema, ema, wt, and asert all have this property (in the case of asert, it's because no prior difficulties are referenced at all). cw and lwma do not have this property. @jtoomim Nice to see the step function test. I agree with @zawy12 that both direction of step function should be tested. The magnitude of the profitability step should be at least as extreme as anything ever seen over the space of an hour or so. |
|
Why is greedy so low? Using last year's miner motivation simulation (6x HR if D is 1.30x baseline HR's needed D and turning off at 1.35x) and if BTC/BCH price is a constant, I see greedy miners with ASERT-484 getting 1% higher target/time (1% more profit) for 1/3 of the blocks (compared to constant miners) and all miners averaging 2.5% profit per block from the slower solvetime. With ASERT-144, the greedy get 1.7% higher target for 1/3 of the blocks but there is not the additional 2.5% lower solvetime being paid out to all miners. My old LWMA N=60 under these conditions has correct solvetime, but this on-off miner scenario gets 7.7% higher target for 1/3 of the blocks. LWMA is also 1.7% at N=288 (ASERT N=144), so it seems I chose N 1/4 or 1/5 of what he needed to be for a lot coins. |
Probably because in my simulation, most of the equilibration is done by the I spent about 5 hours tweaking the |
@dgenr8 Both directions are tested by the code. I had just zoomed in on a positive step in the screenshot. Here's a negative step for you: And here's another one, but with a wider range of ASERT N values so you can taste the rainbow: I've also pushed my LWMA etc code and updated http://ml.toom.im:8051/, so if you want to look at positive and negative steps in more detail, you can do so there. Or, even better, run a copy locally for better performance. It gets pretty laggy when you have a half dozen algorithms with more than 5k blocks each. |
|
I can't understand the inputs to your form very well. My simple method has been able to mimic all the oscillations I've seen. I never thought to try modelling the effect of random changes in exchange price. This might be partly because I want to make random D variation equal price variation. So when I model the effects of miner motivation on random D variation, it's same as price variation if D were constant. So I'm missing the effect of the combination. |
|
I don't have a strong sense of the tradeoffs of high N (stability) vs low N (responsiveness). Qualitatively, excessive stability is dangerous because 1. it leads to more "incorrectly cheap/expensive" blocks when hashrate/price moves around; and 2. a plunge in hashrate (eg post-split) could take days/weeks to recover from, if at all, one of the more realistic "chain death" scenarios. Whereas excessive responsiveness leads to noisy swings in difficulty, which 1. may increase frequency of long confirmations when difficulty bumps too high sometimes, and 2. may be easier for miners to game (though all the good algos here should greatly reduce that).
@dgenr8, was this in response to something I said above? I'd think the nearer an algo is to a pure (memoryless) EMA, the less it should depend on difficulties (or even block times) before the last. So I'm all for avoiding these dependencies when possible. |
|
@jacob-eliosoff As you seem to imply, noisy difficulty itself is not a problem, extreme blocktimes are. The tips of the tightrope walker's pole move crazily so that he can remain steady. This is seen with RTT. You said something about weighting longer times more heavily. I guess it was in reference to something else. Anyway, I agree with you -- that is not justified! |
|
About whether to parameterize based on 2^x or e^x - I went back and forth on this a few times back in the day. I ended up going for e^x because, eg, the EMA where a 1-day-old block has 1/e the weight of a current block, is in some important mathematical sense equivalent to a 1-day SMA - something about how e^x is the only exponential whose integral from -inf to 0 is 1. (The integral of 2^x from -inf to 0 is 1/ln(2) = 1.44, and a 1-day half-life EMA is comparable to a 1.44-day SMA.) But I'm having trouble remembering right now why that's desirable... Though as I recall, 1-day "1/e-life" EMAs did look more comparable on the charts (eg in responsiveness) to 1-day SMA algos like Anyway for our purposes here it doesn't seem like a big deal - between 2^x and e^x is a constant scaling after all. Just worth remembering any time we want to compare "equivalent" EMAs and SMAs. |
OK, I see your point, but this is a questionable definition of short-term greedy. If one of us has to spend money to break down a door so we can all access a vault of gold, then in some theoretical sense it may be rational to wait for someone else to do it. But if no one else does it, it's more rational - even in the short term - to spend the money and break down the door, than to never get the gold. |
Yeah, I wrote half life when I meant mean lifetime.
I hate long variable names, but in this case I would call tau "half_life_in_seconds". The main reason is to show what this constant is and it's relation to what we're doing. To show it's not just some arbitrary value we came up with. I never liked lambda or tau. Especially not lambda because the inverse of this constant is called lambda in both the exponential distribution (which is related to its use here) and the Poisson (which is more remotely related to its use here) and they are connected by this constant. We would be using this "λ" in this context like this: Developers should never choose coin total or emission rate, fees, block time, block size, etc. Those should be determined by proven theory that dictates the code. For example, if you include orphans via a DAG (measure DAG width and increase block time if avg width goes above some value like 1.1) or some other scheme, then you can measure propagation delays which then can continually adjust block time and block size. Market would determine coin emission and fees. In this case, the ideal thing would be to try to let difficulty variation be an indication of exchange rate variation which would dictate half_life_in_seconds, assuming my theory that exchange rate and natural variation should be equal. Maybe more directly, the code should slowly search for a half_life that makes confirmation time as close to avg solvetime as possible. The developer would still have to choose a "rate of search" constant. But getting back to reality, what we could do here is to write half_life as a function of expected daily or weekly exchange rate variation, if my theory that exchange rate and natural variation should be equal is correct (we make that proposal or assumption). Then we look at historical exchange rate data and determine the equation that gives the equivalent half_life. We can almost show ASERT is the one-and-only correct DA. With these 2 theories about what N should be and what the best math is, we've taken our opinions and testing out of the equation in selecting the DA. The code would just contain the theory and we just insert the historical exchange rate number. |
|
Don't forget peer time revert rule has to be reduced from 70 minute to FTL/2 (or did someone tell me BCH does not do it like that?) and be prepared to immediately reject 2x and 1/2 limits or other clipping and median of 3. @jtoomim What are your thoughts on the idea of using the longer form of ASERT target_N+1 = target_MTP * 2^([t_N− 6*T − t_MTP ] / half_life_seconds ) to make it work with Poisson pill? It's interesting that it prevents a negative in the exponential by using MTP and yet it does not have a delay. Also, if the testnet is already using an RTT to go to easy difficulty if the timestamp is > 20 minutes and that presents a problem for ASERT, it seems like a good time to just switch the ASERT to an RTT for that condition. |
|
Can someone give me a simple reason why FTL was supposed to be changed? The only reason I've read so far (from toomims blog) is an attack to lower the difficulty by mining in the future. This attack is something I don't follow. First the actual lowering of difficulty due to mining 70min in future is nothing spectacular and you still need a huge chunk of the hashpower for it to be relevant if you want to create an alternative chain with more actual PoW than the "normal" chain. I don't recall anyone actually posting numbers on this, though. But more importantly, doing secret mining implies you are not held to the FTL rule until you broadcast your block(s). Making the FTL part of this traditional selfish mining attack a rather irrelevant one. You could trivially mine a block a day in the future and then mine for a full day until the time your first block becomes valid is reached and release all you have at that point. See: FTL part is irrelevant to this attack. I don't know if FTL should be lowered, I'd love to see some rationale for it. So far I'm not sure I agree. |
|
A secret mine has to comply with the FTL because the blocks will be rejected if the timestamps are past the FTL. With ASERT's half-life at 416 blocks a selfish mine can get 10 blocks at a 3.5% discount. The 3.5% is not much of a problem compared to the miner doing a 10-block withholding in the first place. So maybe there is no clear need to reduce the FTL unless there is some unforeseen attack. But what's the rationale for keeping it at 2 hours? The revert to peer time rule is 70 minutes which is different from FTL and needs to be about FTL/2 or have peer time removed. |
This is half true. In this case the qualification is super important.
Thanks for sharing that, these numbers are useful to calculate the maximum damage.
That we don't just go changing things unless there is a demonstrated need to change them :)
Ok, then we agree. |
The exception you have in mind is not possible in BCH because of 10-block rule, unless the 10-block rule is attacked. It can be important in coins that do not have the 10-block rule and use SMA or ASERT but not LWMA. In SMA the attacker can get 50% more blocks than the 100% of a simple private mine and 37% more in ASERT. It is super important in coins that have timespan limits (4x and 1/4 in BTC/LTC and 3x & 1/3 in Dash) and do not force sequential timestamps (like Digishield does indirectly with MTP) or otherwise limit how negative the "net solvetime" of each block is (compared to the previous block). In that attack, attacker can get unlimited blocks in < 3x the averaging window. |
|
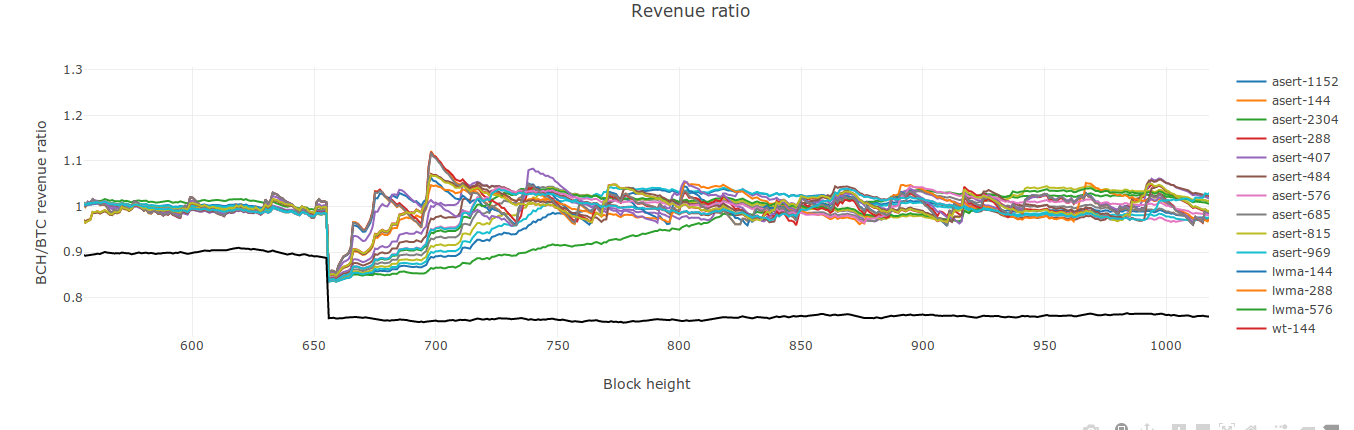
In telegram, zawy12 pointed out an off-by-one error in Mark Lundeberg's ASERT paper. With off-by-one error in the exponent, 20k blocks:
With fix:
So it's pretty inconsequential in terms of performance. (It should only affect the first few blocks after the fork anyway.) But including the fix does save at least 4 bytes in the source code -- a pair of parantheses, and a |
I agree. It's more of a want than a clear need.
There's no need to make this a packaged deal. I think that the FTL should be reduced even if we stick with cw-144, and I think that we should switch to aserti3 or wtema even if we keep the FTL. There is a small synergy for an FTL reduction if we're going to be using an algorithm without a median-of-three prefilter, though. A selfish miner can get a 2.8% difficulty reduction on the 2nd and later blocks in a ≥2-block secret chain/reorg attack with aserti3-416 or wtema-416. A selfish miner can get an 8.3% difficulty reduction on the 3rd and later blocks in a ≥3-block secret chain/reorg attack with cw-144+MTP3. |
|
The usual tradeoff is 1. It's safer to roll out changes separately vs 2. It's easier (and in another sense safer) to fork twice than once. And the usual correct engineering choice is that 1 should take precedence. I think the current FTL is pointless but there's definitely a good argument for leaving out that change for now. |
dear Jonathan, how can I reproduce these plots with the help of your comparison tool at https://github.com/jtoomim/difficulty/tree/comparator ? |
|
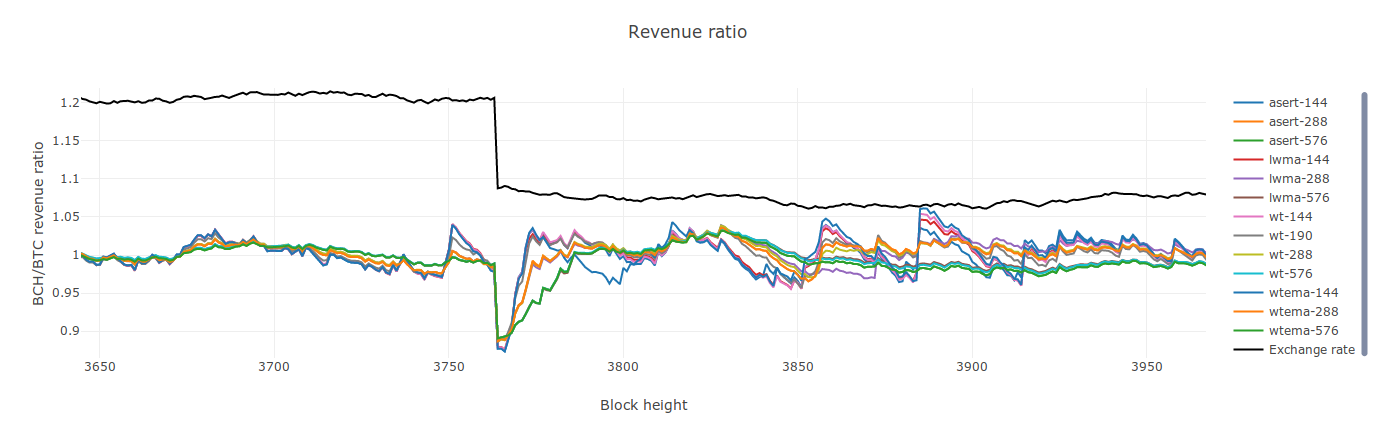
Hi @tromp! That image is just zoomed in a bunch on the revenue ratio graph. There's nothing special about it. Just do a simulation run with the algorithms you want, then take a look at the revenue ratio graph, and click-and-drag to zoom in on a spot where the price (black line) jumps suddenly. E.g.: Zooms to: This zoom doesn't look as pretty as the one you quoted me as doing earlier, but that's just because it doesn't have as many algorithms, and one of them (cw-144) is wacky. |
|
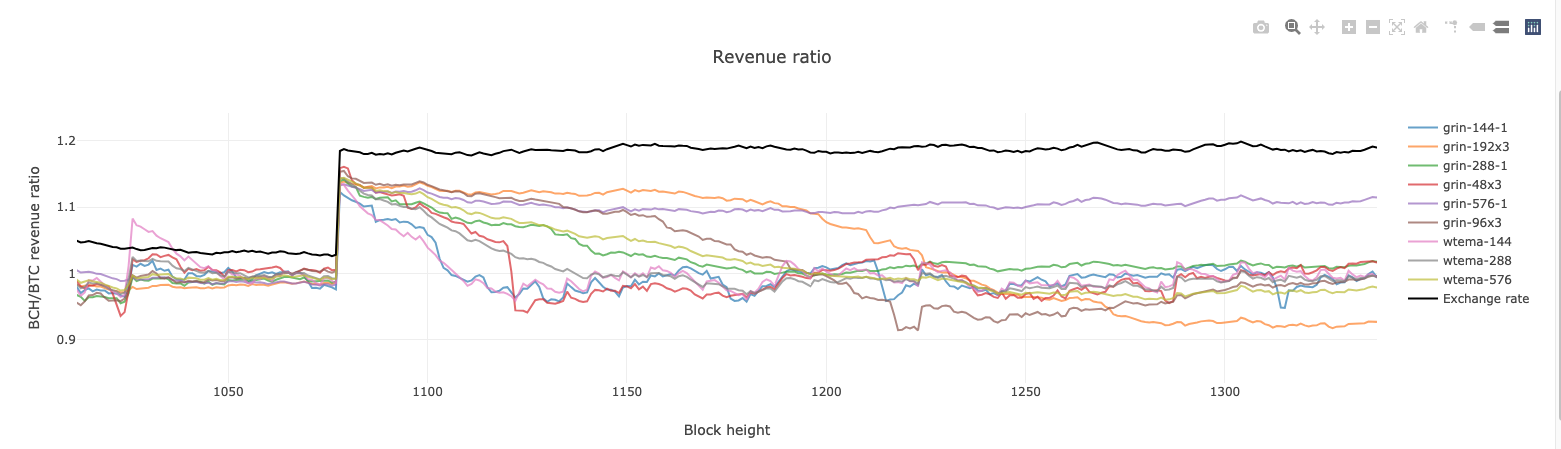
Here's one with several Grin variants: Grin has a damping factor in its DAA
I previously assumed that an n-block d-damped filter had the same half-life as an n*d undamped filter, but the above responsiveness plot appears to contradict that, with e.g. |
I've claimed this in our conversations, so if the idea's wrong I can be blamed. It depends on how you test it. They have the same std dev of difficulties if hashrate is constant. For smallish changes in hashrate I think they will respond similarly. For large changes in hashrate the dampening factor will have a longer delay than this implies to fully reach the change, but respond more in the short term, which gives it a better response than SMA due to the non-linear response of miners. That is, there might be 2x increase in hashrate if diff drops 5% and return to normal after a 10% rise. Dampening with the much smaller averaging window will do the 10% rise more quickly, but then it is stubborn to go higher. SMA responds more slowly then over-responds. I don't understand how an SMA-144 (Grin-144-1) can respond fully in only 50 blocks. What is the 144? I don't like converting to half lives or even the more mathematically pure (e^x) mean lifetimes but just use averaging window lengths and use mean lifetimes for WTEMA/ASERT. What is the averaging window for Grin-48-3? I didn't think it could drop off a cliff like that which is like an SMA. |
|
The grin-48-3 was at a big disadvantage of being at the correct value before the step response. Immediately after the step it drops a lot quickly but then slows up. The gap increases at the end (which I described above as normally being beneficial). |
I 've been changing the naming convention from time to time. I think that any of wtema-120 (i.e. alpha = 1/120), wtema-180, or wtema-240, with a 2 to 4 hour half life, would be good choices for Grin. What do you think? |
|
Yes, that's what I would use. WTEMA alpha=1/180 (mean lifetime-180) will have the stability of Grin-120-3 . It will be noticeably smoother even if you did not currently have oscillations caused be hashrate changes. Jonathan has been wanting 416 for BCH. I think he'll say 208 is at his lower end of acceptability. That is his position on BCH with good liquidity and 10 minute blocks. He might would choose a larger value for 1 minute blocks. I know my LWMA with N=60 has been at least 2x too fast for 2 minute blocks. I should have been using at least 120, and probably 180, if not 360. If LWMA N=180 were at the low end of what you need, especially since its 1 minute blocks, then that would imply WTEMA 1/alpha = 90. Given that Jonathan would opt for at least 200 and I feel safe with 180, I think 180 is good (which is like LWMA N=360). But it's easily possible that 360 better. I know from experience in LWMA that WTEMA-90 is going to work very well (better than my LWMA N=60's) and safe. I believe 2x will work better and still be safe especially with 60 second blocks. Jonathan's point of view is that he knows from testing 2x to 4x (if not higher) is better and safer. Be aware that WTEMA has the same problem as relative ASERT if there are rounding errors. For example, there is a range of nBits that has an average of 1/2 of 2^(-15) truncation error (when it's 3 bytes are from 0x008000 to 0x008FFF). For WTEMA-180 this means 180 * 1/2 * 2^(-15) = 0.27% harder targets and therefore longer solvetimes. Notice the error is 2x if 360 is used. This is if target (or difficulty) is predominantly being rounded either up or down. This amplification of target error does not occur from solvetime error because it is divided by the 180 before it adjusts the target. It should get ahead/behind of the emission schedule if hashrate keeps going up/down in the same way ASERT: I do not know what your future time limit (FTL) is (I'm sure we discussed it before you launched) but I would have it less than the target timespan of 10 blocks if not 1/3 of 1 block. I want to describe my thinking on testing and choosing algorithms. Definitely WTEMA has the best simplicity and performance. The only drawback to LWMA is that a 50% attack for more coins can result in getting 138% instead of 100% of blocks in a given time. This is a real concern for some coins and I've looked for ways to reduce it. I think the best algo is the one that has the fastest response for a given level of stability during constant hashrate. Response speed and stability are conflicting goals because they increase with N and 1/SQRT(N). I rank the algos according to those that have the fastest response to a step change in hashrate for a given Std Dev in difficulty when it has constant hashrate....as long as they don't overshoot. If you overshoot you can have an exponential increase in hashrate. So there should be a bias towards wanting more stability. Once the best algo is "determined", there's the question of how to balance stability and speed. Choosing N is a lot harder than choosing the algorithm. Intuition and experience tells me the stability during constant hashrate needs to be about 1/2 to 1/4 the Std Dev of the exchange rate changes (as it oscillates around an average value for a given week, begining and ending around the same exchange rate so that it does not included long-term upward trends that throw off Std Dev). The idea is that we want to respond as fast as possible without motivating switch mining just from the Std Dev of difficulty (random variation). Miners are looking for lowest difficulty/reward, so an exchange rate change is the same as a difficulty change in terms fo miner motivation. So you could look at historical exchange rate data and choose and N that gives 1/2 to 1/4 the exchange rante Std Dev. Mine and Jonathan/Kyuupichan's testing of miner motivation are very different but generally have the same conclusions. The results seem consistent with the above. |
|
I'd say the choice of time constant for wtema for grin would depend on whether grin is going to be sharing an ASIC hash function or the same hardware with other coins or not, what their relative sizes are, and what the total size of the grin mining economy is. Basically, the questions you need to be asking are: How liquid is the hashpower market? How much do you expect a 1% change in profitability to change hashrate by? Do you expect hashrate vs profitability to be linear, quadratic, exponential, or a threshold function? I.e. do you expect pools like prohashing to jump in for a single block with 10x hashrate, then leave, or do you expect them to slowly allocate hashrate proportionally? When coins get large, their miners tend to use smarter and more game theoretically optimal strategies for competitive hashrate markets. These tend to be more like the "variable" hashrate in my sim. But when coins are small, miners tend to use simple greedy strategies, which is what zawy's sims emphasize. @tromp if you tell me a bit more about grin's current hash markets (or point me to an article or something), I can give you more specific recommendations for simulation parameters and for which types of algorithms are likely to suit you best. @zawy12 Just because I like 416 for BCH does not mean I think it's the best choice for everyone. BCH is huge compared to most of the altcoins you deal with, and the hashrate market is very different. We're probably going to make far more similar recommendations on this one than you expect. |
|
Also, @tromp, do you think it will be easy to get grin to enforce monotonic timestamps (i.e. no negative solvetimes), and maybe restrict the FTL (MAX_FUTURE_BLOCK_TIME, or grin equivalent)? This helps determine which class of algo will be easiest to implement. |
Grin is written from scratch in Rust and doesn't use Bitcoin's nbits encoding.
It's 12 minutes (which is Bitcoin's 2 hour scaled down 10x just as Grin's blocktimes are 10x faster). We will consider changing that along with the DAA to something smaller like 1 minute.
You mean that a 51% attack can not only take all the rewards, but speed up block generation by 38% as well?
Grin aims to be relevant long term, decades from now. We cannot predict the long term exchange rate std dev. |
Grin has an ASIC friendly PoW, and welcomes ASICs, but given that they need 1GB SRAM on-chip for optimal efficiency, they could be many years away until 7nm chips become as affordable as 28nm chips are now. You could do with less onchip SRAM and although efficiency will suffer, it will still vastly outperform a high-end GPU. Right now Grin is the only coin with this PoW, and we hope it will remain the highest daily dollar issuance coin on this PoW for decades to come. The lack of halvings (Grin emission is a constant 1 Grin per second forever) should help here. So in the coming years Grin is at risk of 51% attacks due to rentable GPU hashpower, but should eventually do away with that risk. |
Grin already enforces monotonically increasing timestamps. So we don't have to deal with negative solve times, or with Median Time Past. As mentioned above, FTL is 12 minutes but optionally can be reduced down to 1 minute. |
|
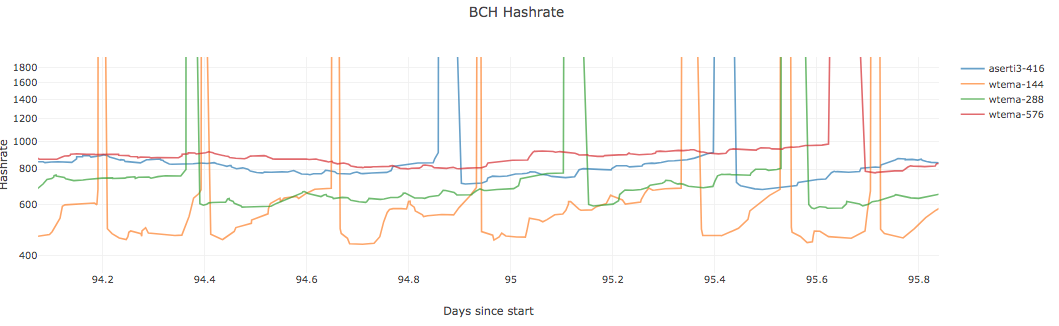
Here is a look at their oscillations: https://grinscan.net/charts The big problem with small coins is that they can have 20x their dedicated hashrate come and go when difficulty changes 10% to 15%. The worst problem ever was Bitcoin Candy that had a miner with 30x their hashrate pushing it up 30% every visit. It just looked like a dead coin when they left and they did it all day. With LWMA N=60 it was never a catastrophic problem (other than BTC Candy) because that meant there would be 1 or 2 blocks that took 7x to 15x too long. Several coins had exactly that kind of 1 or sometimes 2 block delay all day every day. I know of 1 coin that had the persistent oscillation problem and it pretty much went away when they went from LWMA N=60 to LWMA N=120. Based on this direct observation of live results, I feel pretty good about everyone using LWMA N-180 which means WTEMA N=90. But I can't find any modeling that goes against WTEMA N=180. Can you?
Yes.
WTEMA N=90 is going to work on every coin. But judging from my experience in comparing Digishield to LWMA where I saw maybe 25% improvement when they have the same "speed of response ( 60 =~ 17 * 4), Grin with 60 * 3 verses WTEMA N=90 (which is like LWMA/SMA/Grin N=180) will show only will only show about 50% improvement. Going to N=180 I think will give that extra benefit you're looking for without getting into territory that is too unknown for me. The whole problem will be multiple block delays if you have a single big "sticky" miner ("greedy"). If he's < 15x your dedicated hashrate I think it will be OK. I have not tested larger miners yet. |
|
Ok, so Grin is about $25M market cap right now, and it's mostly GPU? I'd guess that if it's mostly GPU, part ASIC, then the ASIC part would be pretty reliable and not a problem, and the GPU stuff would be half reliable, half variable (not greedy). AFAIK, there are a bunch of GPU mining software packages that switch hashrate around on the individual computer level based on individual GPU performance (which varies by algorithm), which means that you're going to get pretty smooth changes in hashrate, rather than the big jumps you get from multipools moving all of their e.g. scrypt hashrate from one minor altcoin to another each block. If that's correct, I'd do simulations with a medium steady hashrate and a decent amount of variable hashrate. With the BCH constants, I'd suggest adding 5000 PH/s of greedy and 2000 PH/s of variable on top of 300 (default) PH/s of steady hashrate for your sims. Make sure you're doing 50k block sims. The presence of the variable miners from GPUs means that you may be able to avoid greedy miners triggering a lot of the time if you have a longer time constant. That will give the variable miners a bit more time to respond, and will make profitability swings usually pretty mild. In these conditions, the 576 and 416 are usually able to avoid having the greedy miners trigger, but the 144 and 288 are not. That makes a pretty big difference. One of the big drawbacks to long N is that the hashrate takes a long time to adjust after a price change. But with a 60 sec/block coin, that's 1/10th as much of an issue as it would be with a 600 sec coin. I'm actually leaning towards 576 or higher here. But I'd like to hear more from @tromp about the mix of ASICs and GPUs, and the intended future miner types, etc. |
|
The problem with testing is that mining conditions can change. But it's possible that N = 1/alpha = 576 is safe for all reasonably legitimate coins that have 60 second blocks. I still have not investigated the variable method to see what I think about it or done my own testing algo that applies when the difficulty stability is significantly less than the exchange rate variation as in these really slow algos. I can only say I feel very safe (in terms of not having long delays and working better than slower algos) with WTEMA 1/alpha=180 in a 60 second coin. If getting stuck is a reason for not going to the slower algos, then my TSA article shows how to make it a safe RTT that adjusts difficulty during the solving if it's taking a long time (but do not used that adjusted difficulty as a basis for future calculations or it can make the 38% much worse). LWMA might be convertible to using only the last 2 blocks if the 38% is a big problem. I could not find a perfectly safe patch for the 38%. The only patch I have is to adjust block time to the T[h] equation I mentioned on the ASERT/NEFDA issue. There's the possibility of adjusting N in the header of each block based on past oscillations, but that will take a fair amount of investigation. |
Closer to $20M, and no evidence of any ASICs yet.
So far, in Grin's 1.5 year history, graphrate (we call it that because each puzzle is a graph) has been surprisingly stable.
I tried that, comparing wtema-120 wtema-240 and wtema-480, and do not see meaningful differences in any scenario. They all have acceptable difficulty fluctuations.
Even these huge order of magnitude graphrate swings lead to smaller difficulty oscillations than we currently suffer.
I don't think I want to go above a 4-hour half life. |
|
So I wrote a script to find the fork block. Kinda annoying that this information is so difficult to find. |












In a previous issue I discussed this in a different way, received feedback from Mark L, and discussed the possibility of RTT for BCH. This issue discusses everything that came up in a live stream and everything I know of surrounding changing BCH's difficulty algorithm (DA).
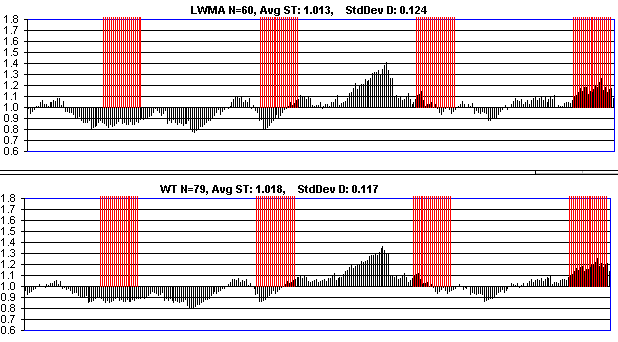
My process to find the "best algo" is this: find a window size parameter "N" for each algo that gives them the same standard deviation for constant HR. This indicates they accidentally attract on-off mining at the same rate. Then simulate on-off mining with step response that turns on and off based on a low and high difficulty value. I have "% delayed" and "% blocks stolen" metrics. Delay: add up a delay qty that is (st - 4xT) for each block over 4xT. Divide that by total blocks to get a % delayed. For "% stolen" I divide time-weighted target that the on-off miner sees by that of dedicated miners. It's how much easier his target was, while he was mining. I just now re-tested 5 DAs. Except for SMA-144, the other 4 below are pretty much the same. WT-190 has slightly lower % stolen but slightly higher delays. (WT-144 is what I kept mistakenly calling wtema in the video). Delays and % stolen are usually a tradeoff. I had been penalizing WT-144 in the past by giving it the same N as LWMA when it needs a larger value.
SMA-144
WT-190 (as opposed to wt-144)
LWMA -144
ASERT / EMA - 72 [ update: See my 2nd comment below. In Jonathan's code, this value would be called 72 * ln(2) ]
I'll advocate the following for BCH in order of importance.
There's also sequential timestamps which might be the hardest to do in reality, but important on a theoretical level. It might be possible to enforce sequential timestamps by making MTP=1 instead of 11. Maybe this could prevent bricking of equipment. Sequential stamps (+1 second) must then be able to override local time & FTL. Overriding local time to keep "messages" (blocks) ordered messages is a requirement for all distributed consensus mechanisms. MTP does this indirectly.
Antony Zegers did some EMA code, using bit-shift for division.
EMA is a close enough approximation to ASERT, but here's Mark's tweet on how to do accurate integer-based e^x.
https://twitter.com/MarkLundeberg/status/1191831127306031104?s=20
wtema simplifies to:
target = prev_target * (1 + st/T/N - 1/N)
where N is called the "mean lifetime" in blocks if it were expressed as ASERT,
target = prev_target * e^(st/T/N - 1/N)
The other form of ASERT should give the same results, but the other form of EMA could return a negative difficulty with a large st.
[ wtema-144 and asert-144 refer to N = 144 / ln(2) = 208.
If wtema is used: Negative solvetimes (st) are a potential problem for wtema if N is small and delays are long and attacker sends an MTP timestamp. See wt-144 code for how to block them. To be sure to close the exploit, you have to go back 11 blocks. Do not use anything like if (st < 0) { st = 0 } in the DA which allows a small attacker to send difficulty for everyone very low in a few blocks by simply sending timestamps at the MTP.
Std Dev of D per N blocks under constant HR for EMA/ASERT is ~1/SQRT(2*N). This is important for deciding a value for N. If HR increases 10x based on 10% drop in D, you definitely want N > 50 or the DA is motivating on-off mining. On the other hand, being at the edge of motivating on-off mining can reduce the expected variation in D. BTG's Std Dev is about 0.10 when it would have been 0.15 if HR was constant (N=45 LWMA, N=22.5 in ASERT terms). So it's paying a little to on-off miners to keep D more constant. ASERT with N=72 is same as SMA=144 in terms of D variation when HR is constant.
On the other side is wanting a sufficiently fast response to price changes. As a starting point, for ASERT N=100 it takes 6 blocks to rise 5% in response to a 2x increase in HR. This seems sufficiently fast. Std Dev is 1/SQRT(2*100) = 7% per 100 blocks which seems high. 5% accidental changes in D seems to motivate substantial HR changes, so maybe N=200 is better which will have 5% variation per 200 blocks. But this is like LWMA N=400 which would be incredibly smooth and nice if it works but this is 3x larger than my experience. BTG is very happy with LWMA N=45 with Std Dev 10%. Notice that there's bigger bang for the buck with lower N due to the 1/SQRT(N) verses N. You get more speed than you lose stability as you go to lower N. So instead of 200, I would go with 100 or 150.
None of the 60 or so LWMA coins got permanently stuck. About 5% could not get rid of bothersome oscillations. When sending the same random numbers to generate solvetimes, LWMA / EMA / ASERT are almost indistinguishable, so I do not expect them to get stuck either. Most LWMA's are N=60 which has the stability of EMA with N=30. N=100 would have probably been a lot nicer for them, if not N=200 (ASERT N=100). They are mostly T = 120 coins, so they have very fast response, reducing the chances of getting stuck.
Mark was concerned about forwarded timestamps sending difficulty very low which could allow a small attacker to do a spam attack (he would begin with setting a far-forwarded stamp for EMA/ASERT for submission later). To make this a lot harder to so, use st = min(st, 7*600). So long delays will not drop the difficulty as much as "it wants to". Most LWMA's do this as an attempt to reduce oscillations but it may not have helped any.
Combining upper and lower limits on difficulty, timespan, or solvetimes like the 4x and 1/4 in BTC, and the 2 and 1/2 in BCH is what allows unlimited blocks in < 3x the difficulty window. I'm the only one I know of that has described it. A couple of coins following me were the first to see it, losing 5,000 blocks in a couple of hours because I had the hole in LWMA but did not realize it. Some LWMA's had symmetrical limits on st, not just the 7xT upper limit. Removing the 1/2 limit on timespan in BCH will prevent it.
If FTL is dropped, the 70 minute revert from peer to local time rule should be removed (best) or set it to FTL/2 or less. It should be coded as function of FTL. There are a couple of exploits due to Sybil or eclipse attacks on peer time.
A pre-requisite for BFT is that all nodes have a reliable clock that has higher security than the BFT. The clock in POW is each node operator knowing what time it is without needing to consult the network. Any node can unilaterally reject a chain if its time is too far in the future so it's impervious to 99.99999% attacks. (Although current mining on honest chain needs to be > 50% HR of the forwarded cheating chain for the node to continue to reject the cheating chain because time going forward can make the cheating chain become valid.)
The text was updated successfully, but these errors were encountered: